文章目录(Table of Contents)
Dropout在做什么
Train时Dropout在做什么
当dropout(p)时,意味着每个neuron, 有p%的可能性被去除;(这里需要注意的是,不是去除p%的neuron)
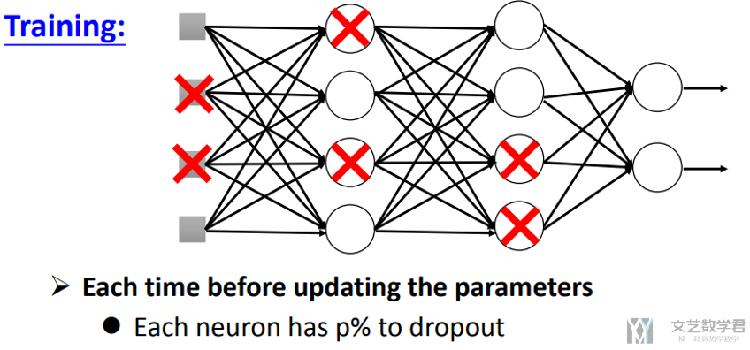
我们可以看到的是,每一次进行dropout的时候,网络的结构都会发生改变,会变成一个比之前thin的网络结构。
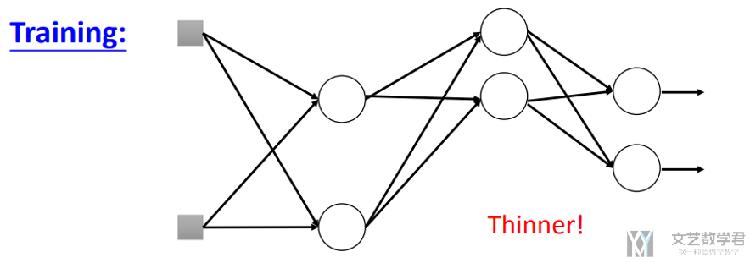
所以,总结一下:dropout在训练的时候步骤如下:
- 每次前向传播时, 去除一些neuron;
- 网络的结构发生了改变;
- 使用新的网络结构进行训练;
- 对于每一个min-batch, 每次都会修改网络的结构;
Test时Dropout在做什么
在进行test的时候,我们是不进行dropout,同时要修改之前的系数,我们看一下具体的步骤。
- 不进行dropout(即每个节点都不会被去掉);
- 同时, 若train时dropout(p), 则在test时候, 所有系数需要乘(1-p%);
- 例如, dropout(0.9), 则最后所有系数需要乘(1-0.9);
下面我们来解释一下为什么最后所有系数要乘(1-p%),他的最终的目标是为了保持不进行dropout时候网络输出的值与进行dropout时,网络输出值的期望相同。我们看下面一个具体的例子:
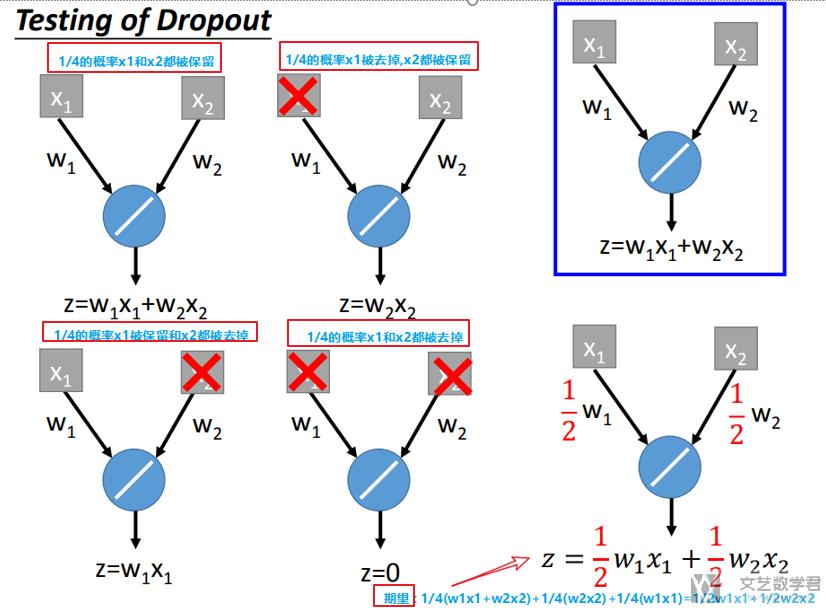
上图中,我们的Dropout(0.5)。则每个点有50%的可能性被去掉。
原始的结构如蓝框所示,则dropout后会有四种不同的可能性,分别如图左边的四个小结构所示,其中每个结构的可能性都是1/4.
我们对上面可能的四个结构的输出求期望,得到1/2×w1×x1+1/2×w2×x2,相当于在原始的网络的系数上都乘了(1-0.5)。这也就是为什么在最后进行test的时候,所有的系数都需要乘上(1-p)了。
对于线性结构来说,我们都是可以这么进行计算的,即dropout和最后系数乘(1-p)是等价的。这样大概解释了一下为什么最后系数要乘(1-p).
Pytorch手动实现Dropout
上面我们看了dropout在train和test上的一些应用, 下面我们不使用Pytorch提供你的dropout, 自己实现一遍.
在上面我们讲了, 在test的模式下面, 最后的系数需要乘上(1-p), 其实我们可以直接对数据X做修改, 如果上一层网络的输出是X, 那么在dropout输出的时候, 没有被dropout的点, 我们除(1-p). 例如还是上面的情况, 此时四个图最后的输出分别是:
- z = 2×w1×x1+2×w2×x2
- z = 2×w1×x1
- z = 2×w2×x2
- z = 0
最终的期望是z = w1×x1+w2×x2, 此时test模式就不需要进行改变. 我们按照这个思想, 可以写出如下的dropout的函数.
- def dropout_layer(X, dropout):
- assert 0 <= dropout <= 1
- # In this case, all elements are dropped out
- if dropout == 1:
- return torch.zeros_like(X)
- # In this case, all elements are kept
- if dropout == 0:
- return X
- mask = (torch.Tensor(X.shape).uniform_(0, 1) > dropout).float()
- return mask * X / (1.0-dropout)
我们进行一下简单的测试, 可以看到在dropout=0.5的情况下, 最后保留下来的值, 都会被乘2.
- X= torch.arange(16, dtype = torch.float32).reshape((2, 8))
- print(X)
- """
- tensor([[ 0., 1., 2., 3., 4., 5., 6., 7.],
- [ 8., 9., 10., 11., 12., 13., 14., 15.]])
- """
- print(dropout_layer(X, 0.5))
- """
- tensor([[ 0., 0., 0., 0., 8., 10., 0., 14.],
- [16., 18., 0., 22., 0., 26., 0., 30.]])
- """
于是, 我们在设计网络的时候, 只需要在测试的时候去除dropout即可, 就不需要更改模型的系数了.
- class Net(nn.Module):
- def __init__(self, num_inputs, num_outputs, num_hiddens1, num_hiddens2, is_training = True):
- super(Net, self).__init__()
- self.num_inputs = num_inputs
- self.is_training = is_training
- self.lin1 = nn.Linear(num_inputs, num_hiddens1)
- self.lin2 = nn.Linear(num_hiddens1, num_hiddens2)
- self.lin3 = nn.Linear(num_hiddens2, num_outputs)
- self.relu = nn.ReLU()
- def forward(self, X):
- H1 = self.relu(self.lin1(X.reshape((-1, self.num_inputs))))
- # Use dropout only when training the model
- if self.is_training == True:
- # Add a dropout layer after the first fully connected layer
- H1 = dropout_layer(H1, dropout1)
- H2 = self.relu(self.lin2(H1))
- if self.is_training == True:
- # Add a dropout layer after the second fully connected layer
- H2 = dropout_layer(H2, dropout2)
- out = self.lin3(H2)
- return out
Dropout有用的一种解释
Dropout相当于是一种ensemble的技术,因为每一个batch训练的网络结构是不同的,所以最终结果相当于是很多网络结构的ensemble.
同时,相较于传统的ensemble,dropout的不同的结构之间又是贡献参数的,这样可以使得模型的训练速度更加快。
要注意的是
- dropout需要样本量比较多;
- 在过拟合的时候使用dropout技术,即training set上很好, testing set上结果不好。
- 在使用dropout的时候,可以适当增加模型的层数(复杂度)
Dropout的具体实现
在pytorch中,dropout在train和test的时候不会改变系数,他会直接在训练的时候,将dropout层的输出的值,除(1-p),这样就不需要改变系数了。在test的时候只需要不进行dropout即可。
下面是一个简答的测试结果的图片:

我们看到,在dropout(0.9),且在train模式下,输出的值会直接乘10,相当于除(1-0.9)。在test的时候,就会直接关闭dropout。
在pytorch中,我们可以通过如下的方式控制model是train还是test模式:
- model.train() # Set model to training mode
- model.eval() # Set model to evaluate mode
这个时候使用nn.Dropout是一个比较好的选择。
Pytorch实验
下面我们使用Pytorch进行实验,测试dropout的效果。
实验测试代码可以查看:Pytorch模型实例-MNIST dataset,下面放一下实验结果图。
网络结构
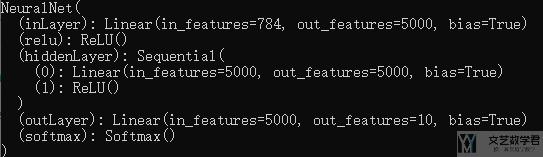
不使用Dropout技术
每一个epoch的准确率变化,在验证集上大概会在90%左右。
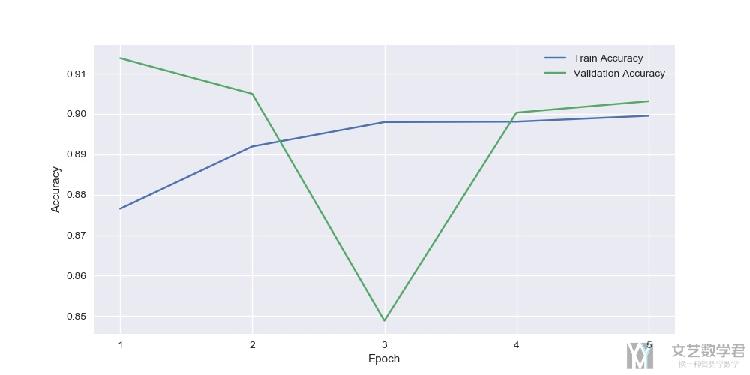
最终在测试集上的准确率如下所示:

使用Dropout技术
使用dropout技术后,每个epoch的验证集的准确率变化如下所示:
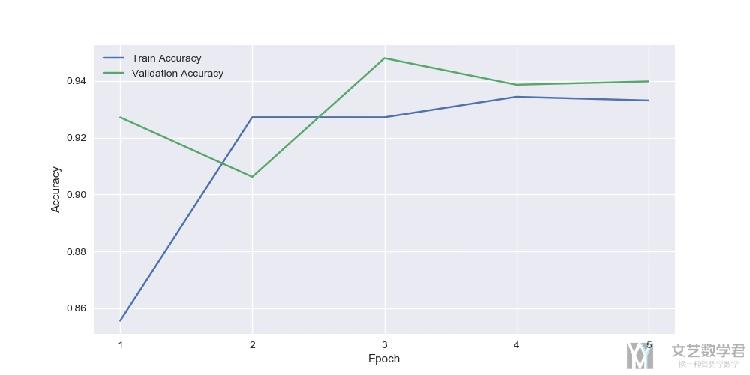
在看一下在test上的效果,效果会比不使用dropout要好上一些:

结语

需要注意的是,dropout技术是用在过拟合的时,即能在training set上得到好的结果。我们在使用之前一定要进行判断,是过拟合了还是欠拟合。
如果model在training set上结果就不好,使用dropout技术也不能带来好的结果。
- 微信公众号
- 关注微信公众号
-

- QQ群
- 我们的QQ群号
-













评论