Batch Normalization技术介绍

Batch Normalization工作原理

首先，我们输入的是一个batch，下面的例子中，我们可以将(x1,x2,x3)看成一个Batch。

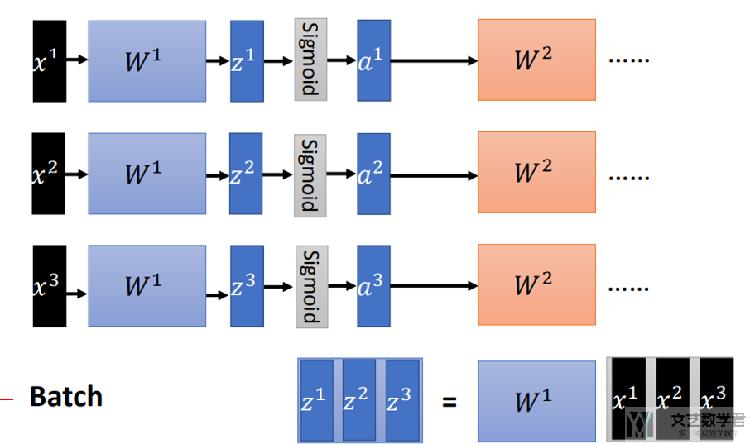
接着，我们计算在经过一层网络后, 输出值(z1,z2,z3)的均值和标准差，如下图所示：

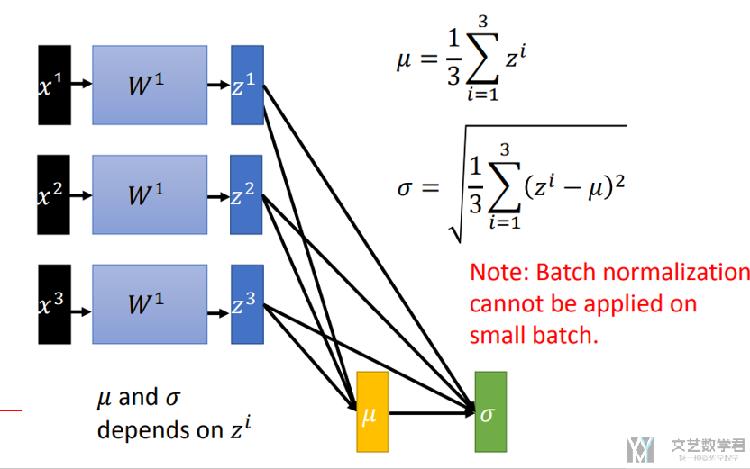
接着，对(z1,z2,z3)进行标准化，标准化后z的均值为0，方差为1;

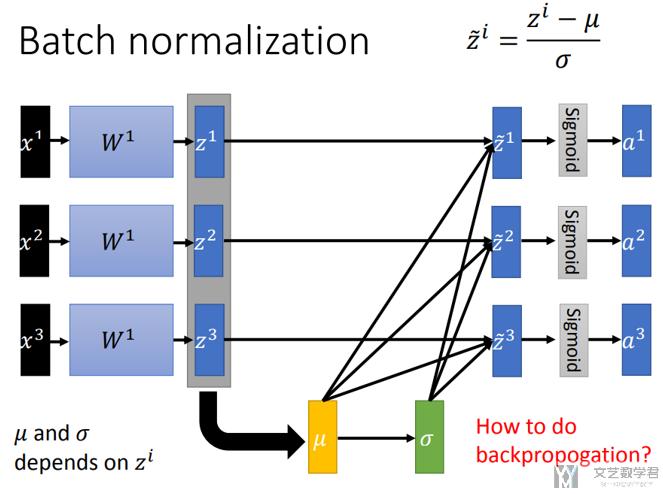
最后，我们的输出为 z=A*z' + B，其中A和B是需要学习的参数, 这里A和B是包含在Batch Normalization层的参数; 例如我们直接查看Pytorch中BN层的参数, 可以发现是有weight和bias的.

我们注意到，当A=标准差, B=均值, 则相当于z_new = z，即相当于没有进行batch normalization.

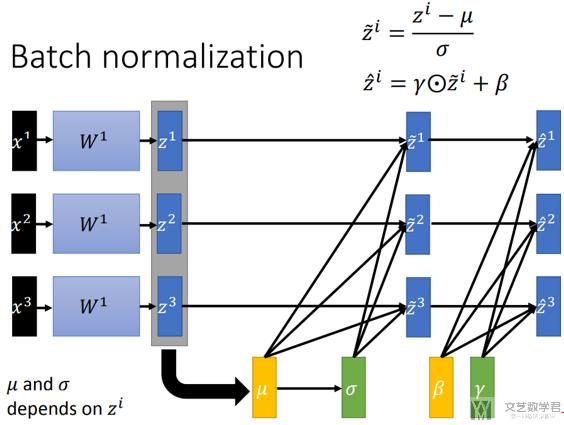
需要注意

• Batch Normalization不能在小数据集上进行，因为均值和方差的估计会不准确。
• 在test上时，不会计算test的均值与方差，会使用trian时候均值方差的移动平均来代替（下面会有一个例子）；

Batch Normalization实际使用

在batch normalization的时候，我们在train和test的时候进行的操作是不同的。这是由于在test的时候, 输入数据可能只有一个data, 故不能计算均值和标准差;

所以, 在test的时候, 会使用之前计算得到的均值和标准差做标准化。

初始化参数

首先，我们先初始化一些参数，下面初始化的有我们的测试数据X，测试数据的均值方差，迭代式子里最初的均值方差(均值0，方差1)，和迭代的公式。

迭代计算过程

下面看一下在输入是X的情况下，在训练模式下的输出结果和在测试模式下的输出结果。

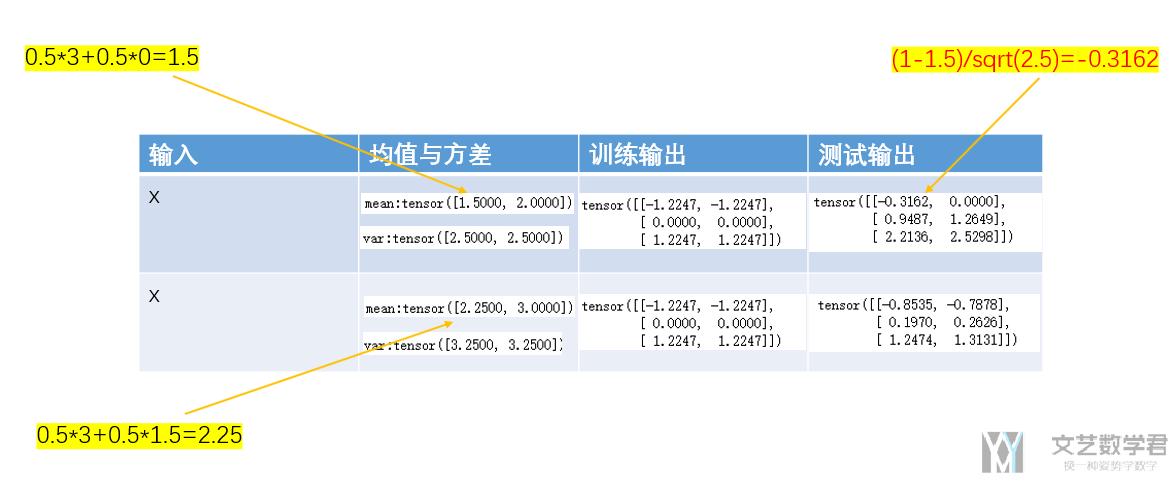
可以看到，在训练模式下，pytorch会对原始数据进行标准化，同时更新均值与方差（这个均值与方差是在test的时候，对test数据进行标准化的）。

在测试模式下，会使用在训练模式下反复计算的均值和方差来进行标准化。具体的计算过程可以结合上面的图进行推导。

第一行是第一次输出X后不同的输出，第二行是第二次输入X后不同的输出。

测试代码

把测试代码放在下面，方便自己测试。

Batch Normalization的手动实现

为了能够更好的说明Batch Normalization, 我们手动实现一下Batch Norm的功能. 首先是实现计算Batch Norm的函数, 包含:

• moving_mean和moving_var的计算;
• 包含在训练模式和测试模式下对X进行标准化;
• 同时, 这里会有两个参数, 分别是gamma和beta, 是需要在训练的时候进行更新的;

定义了上面计算的函数之后, 下面就是定义BatchNorm layer. 这里会存储moving_mean和moving_var, 会存储参数gamma和beta.

上面计算过程与实际的layer分开的过程, 是非常好的. (This pattern enables a clean separation of math from boilerplate code.)

直接使用Pytorch中的BatchNorm

上面我们自己动手实现了BatchNorm的相关操作, 但是在实际情况中, 我们会直接使用框架中现成的函数, 这样使用起来就会方便很多. 下面我们将LeNet加上BatchNorm, 注意我们在全连接层的部分也是可以增加一维的BatchNorm的,  整体的代码如下所示:

Batch Normalization实验

之前在dropout的实验里，我们可以看到使用dropout后，准确率变化如下所示：

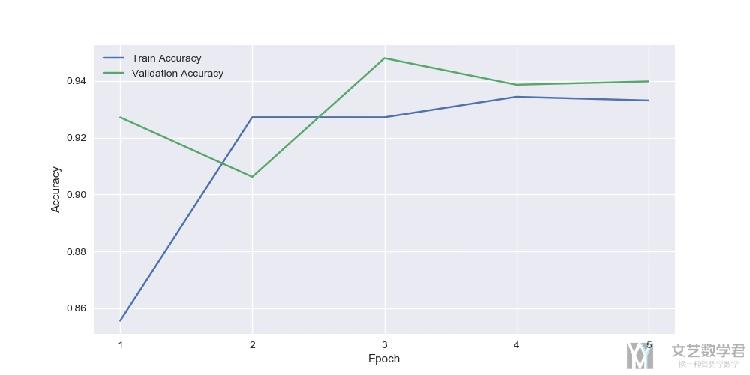
在使用batch normalization后，我们可以看到准确率有了进一步的提升：

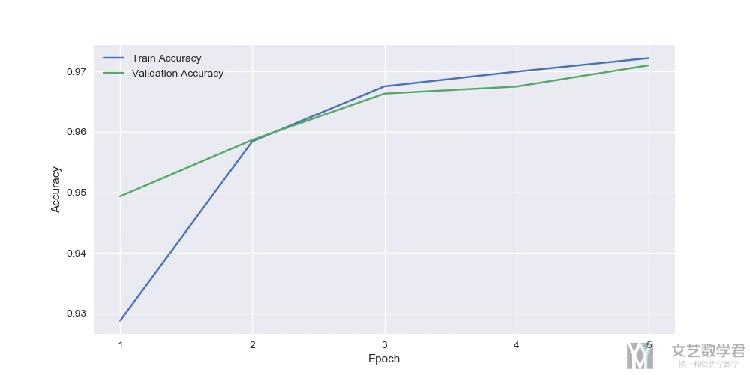
原始模型train不起来

我们看一下原始模型训练不起来的情况，如下图所示，在训练集上准确率只有10%左右

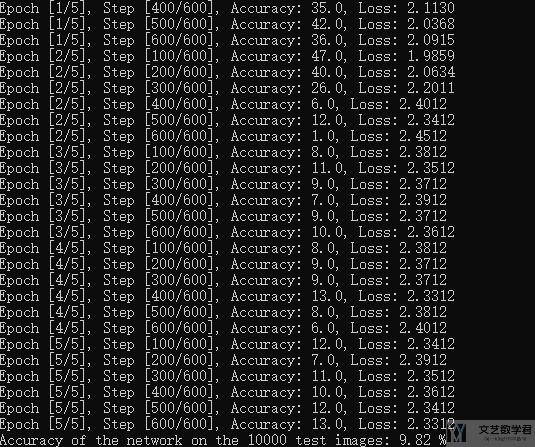
在使用batch normalization后，模型在训练集上的准确率可以提升到80%以上；

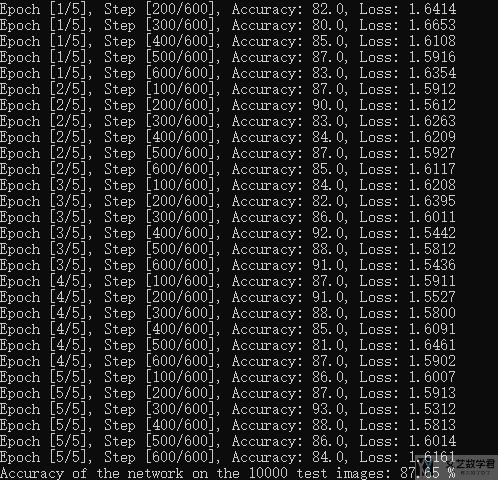
结语

数据标准化是很重要的一步，会对模型最终的好坏起到至关重要的作用。Batch Normalization在model无法train起来的时候，也就是在训练集上结果很差的时候，会起到比较好的作用。