GRU for Time Series in Pytorch–Pytorch实现时间序列分析

王 茂南
王 茂南
王 茂南
3080
文章
75
评论
2019年6月8日07:38:31152 9776字阅读32分35秒
摘要这一篇文章会介绍使用RNN来完成时间序列的分析，更准确的说是时间序列的预测。本篇内容会介绍使用GRU来预测AR(5)的数据。

简介

这一篇文章，会完成使用RNN, 更具体的说是使用GRU来实现时间序列的分析, 用来做预测. 最终的效果如下, 后面会有每一步的具体步骤。

GRU for Time Series in Pytorch–Pytorch实现时间序列分析

主要参考的文章为下面两篇文章 :

数据输入

在处理时间序列数据的时候，对于输入我们有两种处理的办法。我们会将数据分为chunk。

如图一, 比如我们使用前6天预测第七天, 再使用前七天预测第八天, 以此类推.

如图二, 比如我们使用0-6天预测第七天, 使用1-7天预测第八天, 以此类推.

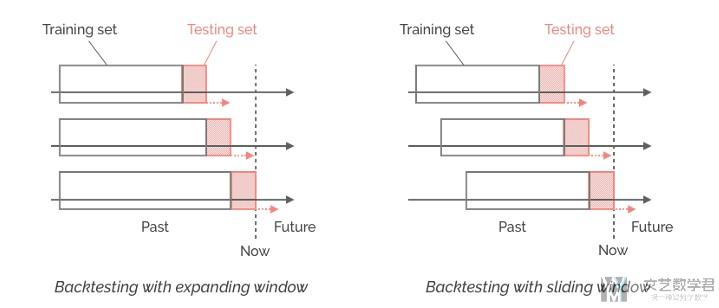
GRU for Time Series in Pytorch–Pytorch实现时间序列分析

在我们这篇文章，我们会采取使用图2的形式. 我们会以7天作为一个阶段, 使用七天的数据预测第八天.

In our case study, I will use samples consisting of 7-days sliding windows with step size equal to 1, used to predict the next value (1-step ahead forecast).

下面我们看一下具体的实现。这里一段内容参考自上面的链接二。

具体的实现

导入所需要的库

  1. import torch
  2. import torch.nn as nn
  3. import torch.optim as optim
  5. import numpy as np
  6. from sklearn.model_selection import train_test_split
  7. import matplotlib.pyplot as plt

Generating Autoregressive data for experiments(生成所需要的数据)

这里的代码来自上面的链接一, 我在代码注释中也写了来源, 这个数据我没仔细看, 后面就是直接使用了。

  1. # 代码来源 : http://www.jessicayung.com/generating-autoregressive-data-for-experiments/
  2. # 代码来源 : https://github.com/jessicayung/blog-code-snippets
  3. class TimeSeriesData:
  4.     def __init__(self, num_datapoints, test_size=0.2, max_t=20, num_prev=1,
  5.                  noise_var=1):
  6.         """
  7.         Template class for generating time series data.
  8.         :param test_size: in (0,1), data to be used in test set as a fraction of all data generated.
  9.         """
  10.         self.num_datapoints = num_datapoints
  11.         self.test_size = test_size
  12.         self.num_prev = num_prev
  13.         self.max_t = max_t
  14.         self.data = None
  15.         self.noise_var = noise_var
  16.         self.y = np.zeros(num_datapoints + num_prev*4) # TODO: check this
  17.         self.bayes_preds = np.copycopy(self.y)
  19.         # Generate data and reshape data
  20.         self.create_data()
  22.         # Split into training and test sets
  23.         self.train_test_split()
  25.     def create_data(self):
  26.         self.generate_data()
  27.         self.reshape_data()
  29.     def generate_data(self):
  30.         """Generates data in self.y, may take as implicit input timesteps self.t.
  31.         May also generate Bayes predictions."""
  32.         raise NotImplementedError("Generate data method not implemented.")
  34.     def reshape_data(self):
  35.         self.x = np.reshape([self.y[i:i + self.num_prev] for i in range(
  36.             self.num_datapoints)], (-1, self.num_prev))
  37.         self.y = np.copycopy(self.y[self.num_prev:])
  38.         self.bayes_preds = np.copycopy(self.bayes_preds[self.num_prev:])
  40.     def train_test_split(self):
  41.         test_size = int(len(self.y) * self.test_size)
  42.         self.data = [self.X_train, self.X_test, self.y_train,
  43.                      self.y_test] = \
  44.                     self.x[:-test_size], self.x[-test_size:], \
  45.                     self.y[:-test_size], self.y[-test_size:]
  46.         self.bayes_preds = [self.bayes_train_preds, self.bayes_test_preds] = self.bayes_preds[:-test_size], self.bayes_preds[-test_size:]
  48.     def return_data(self):
  49.         return self.data
  51.     def return_train_test(self):
  52.         return self.X_train, self.y_train, self.X_test, self.y_test
  54. class ARData(TimeSeriesData):
  55.     """Class to generate autoregressive data."""
  57.     def __init__(self, *args, coeffs=None, **kwargs):
  58.         self.given_coeffs = coeffs
  59.         super(ARData, self).__init__(*args, **kwargs)
  61.         if coeffs is not None:
  62.             self.num_prev = len(coeffs) - 1
  64.     def generate_data(self):
  65.         self.generate_coefficients()
  66.         self.generate_initial_points()
  68.         # + 3*self.num_prev because we want to cut first (3*self.num_prev) datapoints later
  69.         # so dist is more stationary (else initial num_prev datapoints will stand out as diff dist)
  70.         for i in range(self.num_datapoints+3*self.num_prev):
  71.             # Generate y value if there was no noise
  72.             # (equivalent to Bayes predictions: predictions from oracle that knows true parameters (coefficients))
  73.             self.bayes_preds[i + self.num_prev] = np.dot(self.y[i:self.num_prev+i][::-1], self.coeffs)
  74.             # Add noise
  75.             self.y[i + self.num_prev] = self.bayes_preds[i + self.num_prev] + self.noise()
  77.         # Cut first 20 points so dist is roughly stationary
  78.         self.bayes_preds = self.bayes_preds[3*self.num_prev:]
  79.         self.y = self.y[3*self.num_prev:]
  81.     def generate_coefficients(self):
  82.         if self.given_coeffs is not None:
  83.             self.coeffs = self.given_coeffs
  84.         else:
  85.             filter_stable = False
  86.             # Keep generating coefficients until we come across a set of coefficients
  87.             # that correspond to stable poles
  88.             while not filter_stable:
  89.                 true_theta = np.random.random(self.num_prev) - 0.5
  90.                 coefficients = np.append(1, -true_theta)
  91.                 # check if magnitude of all poles is less than one
  92.                 if np.max(np.abs(np.roots(coefficients))) < 1:
  93.                     filter_stable = True
  94.             self.coeffs = true_theta
  96.     def generate_initial_points(self):
  97.         # Initial datapoints distributed as N(0,1)
  98.         self.y[:self.num_prev] = np.random.randn(self.num_prev)
  100.     def noise(self):
  101.         # Noise distributed as N(0, self.noise_var)
  102.         return self.noise_var * np.random.randn()
  104. # A set of coefficients that are stable (to produce replicable plots, experiments)
  105. fixed_ar_coefficients = {2: [ 0.46152873, -0.29890739],
  106.     5: [ 0.02519834, -0.24396899,  0.2785921,   0.14682383,  0.39390468],
  107.                         10: [-0.10958935, -0.34564819,  0.3682048,   0.3134046,  -0.21553732,  0.34613629,
  108.   0.41916508,  0.0165352,   0.14163503, -0.38844378],
  109.                          20: [ 0.1937815,   0.01201026,  0.00464018, -0.21887467, -0.20113385, -0.02322278,
  110.   0.34285319, -0.21069086,  0.06604683, -0.22377364,  0.11714593, -0.07122126,
  111.  -0.16346554,  0.03174824,  0.308584,    0.06881604,  0.24840789, -0.32735569,
  112.   0.21939492, 0.3996207 ]}

使用上面的代码生成我们需要的数据, 这样我们就有了训练和测试的时候需要的数据了。

  1. #####################
  2. # Generate data
  3. #####################
  4. num_datapoints = 100
  5. test_size = 0.2
  6. input_size = 20
  7. noise_var = 0
  9. data = ARData(num_datapoints, num_prev=input_size, test_size=test_size, noise_var=noise_var, coeffs=fixed_ar_coefficients[input_size])
  11. # --------------------
  12. # Device configuration
  13. # --------------------
  14. device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
  16. # data for train and test
  17. X_train = torch.from_numpy(data.X_train).float().to(device)
  18. X_test = torch.from_numpy(data.X_test).float().to(device)
  19. y_train = torch.from_numpy(data.y_train).float().to(device)
  20. y_test = torch.from_numpy(data.y_test).float().to(device)

 定义生成器(用于逐次生成训练的数据)

根据上面我们介绍的，我们需要每七天的数据作为一组，进入模型进行训练. 如我们需要逐次返回 :

  • 3/1-3/7的数据为训练集, 3/8为需要预测的；
  • 3/2-3/8的数据为训练集, 3/9为需要预测的
  • 3/3-3/9的数据为训练集, 3/10为需要预测的
  • ...

于是我们使用yield, 最后可以返回一个生成器.

  1. # 使用slide window, window size=7
  2. # 即返回 data=1-7 label=8; data=2-8 label=9
  3. def create_dataset(X_data, y_data, look_back=1):
  4.     length = X_data.size(0)
  5.     for i in range(0,length-look_back):
  6.         result = (X_data[i:(i+look_back),:],y_data[i+look_back])
  7.         yield result

简单测试一下，就是可以逐次返回训练的样本和target.

  1. test_data = create_dataset(X_train,y_train, look_back=7)
  2. for (i,j) in test_data:
  3.     print(i.shape,j)
GRU for Time Series in Pytorch–Pytorch实现时间序列分析

定义网络

接下来我们定义预测所需要的网络结构。

  1. class TimeSeries(nn.Module):
  2.     def __init__(self, input_dim, hidden_dim, batch_size, output_dim=1, num_layers=2):
  3.         super(TimeSeries,self).__init__()
  4.         self.input_dim = input_dim # 输入的特征的个数
  5.         self.hidden_dim = hidden_dim
  6.         self.batch_size = batch_size
  7.         self.num_layers = num_layers
  8.         self.output_dim = output_dim
  10.         # Defeine the GRU layer
  11.         self.gru = nn.GRU(self.input_dim, self.hidden_dim, self.num_layers, dropout=0.1)
  12.         # Define the output layer
  13.         self.fc = nn.Linear(self.hidden_dim, self.output_dim)
  15.     def init_hidden(self):
  16.         # initialise hidden state
  17.         return (torch.zeros(self.num_layers, self.batch_size, self.hidden_dim).to(device))
  18.         # return (torch.zeros(self.num_layers, self.batch_size, self.hidden_dim))
  20.     def forward(self,x):
  21.         self.batch_size = x.size(1)
  22.         self.hidden = self.init_hidden() # 初始化hidden state
  23.         gru_out, self.hidden = self.gru(x, self.hidden)
  24.         y_pred = self.fc(gru_out[-1])
  25.         return y_pred

简单测试一下网络的编写是否是正确的。

  1. # 模型的测试
  2. input_data = torch.from_numpy(np.random.randn(7,1,20)).float().to(device)
  3. model = TimeSeries(input_dim=20, hidden_dim=20, batch_size=1, output_dim=1, num_layers=2).to(device)
  4. model(input_data)
  5. """
  6. tensor([[-0.0021]], device='cuda:0', grad_fn=<AddmmBackward>)
  7. """

模型的训练

准备好模型和数据之后，我们就可以开始训练了。训练的代码如下所示：

  1. # 模型的初始化
  2. model = TimeSeries(input_dim=20, hidden_dim=28, batch_size=1, output_dim=1, num_layers=3).to(device)
  4. # 定义损失函数和优化器
  5. criterion = nn.MSELoss()
  6. optimizer = optim.Adam(model.parameters(),lr=0.001)
  8. # 模型的训练
  9. pre_output = y_train.clone()
  10. num_epochs = 1000
  11. hist = np.zeros(num_epochs) # 用来记录每一个epoch的误差
  13. for t in range(num_epochs):
  14.     test_data = create_dataset(X_train,y_train, look_back=7) # 这个要每次刷新
  15.     loss = torch.tensor([0.0]).float().to(device)
  16.     for num, (i,j) in enumerate(test_data):
  17.         optimizer.zero_grad()
  18.         # reset hidden states
  19.         model.hidden = model.init_hidden()
  20.         # forward
  21.         output = model(i.unsqueeze(1))
  22.         pre_output[num+7]=output
  23.         # backward
  24.         loss = loss + criterion(output, j)
  25.     loss.backward()
  26.     # optimize
  27.     optimizer.step()
  28.     # 打印与记录误差
  29.     if t%10 == 0:
  30.         print("Epoch:{:0>4d}, MSE:{:<10.9f}".format(t,loss.item()))
  31.         print('============')
  32.     hist[t] = loss.item()

基本都是常规的操作，有两个需要注意一下：

  • 不是每次都进行反向传播和系数的优化, 我们会把一个epoch所有的loss求和, 一起进行反向传播.
  • 还有一点要注意的是, create_dataset需要写在epoch的循环里面, 可以理解一下为什么.
GRU for Time Series in Pytorch–Pytorch实现时间序列分析

结果的可视化

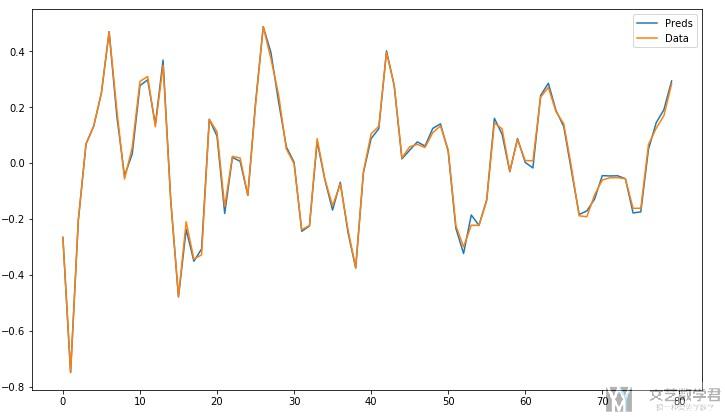
在这里我没在测试集上做测试, 就直接看一下训练集的效果。首先看一下预测的值与实际值画的图 :

  1. # 打印预测和实际
  2. fig = plt.figure(figsize=(12,7))
  3. ax = fig.add_subplot(1,1,1)
  5. ax.plot(pre_output.cpu().detach().numpy(), label="Preds")
  6. ax.plot(y_train.cpu().detach().numpy(), label="Data")
  7. ax.legend()
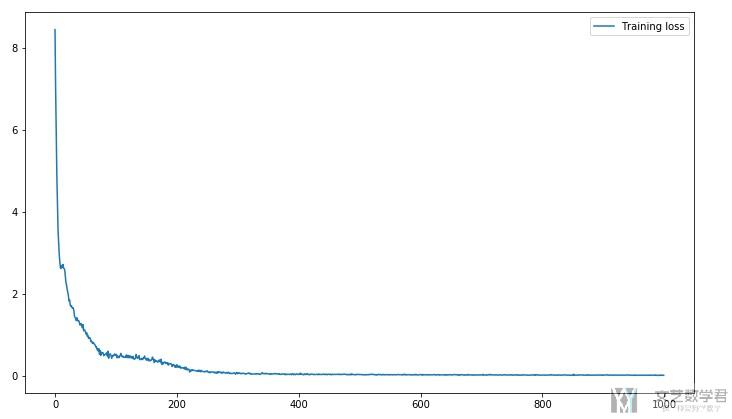
GRU for Time Series in Pytorch–Pytorch实现时间序列分析

接着看一下训练过程中Loss的变化的过程 :

  1. # 打印Loss
  2. fig = plt.figure(figsize=(12,7))
  3. ax = fig.add_subplot(1,1,1)
  5. ax.plot(hist, label="Training loss")
  6. ax.legend()

大概在300个epoch的时候，就已经到较好的效果了。

GRU for Time Series in Pytorch–Pytorch实现时间序列分析

结语

上面是关于使用Pytorch来实现时间序列的预测，完整的notebook可以参考下面的链接。

RNN for Time Series in Pytorch

  • 微信公众号
  • 关注微信公众号
  • weinxin
  • QQ群
  • 我们的QQ群号
  • weinxin
王 茂南
  • 本文由 发表于 2019年6月8日07:38:31
  • 转载请务必保留本文链接：https://mathpretty.com/10537.html
匿名

发表评论

匿名网友 填写信息

:?: :razz: :sad: :evil: :!: :smile: :oops: :grin: :eek: :shock: :???: :cool: :lol: :mad: :twisted: :roll: :wink: :idea: :arrow: :neutral: :cry: :mrgreen:

评论：15   其中：访客  9   博主  6
    • 老学生
      老学生
      2021年1月15日 上午10:37 1F
      回复

      代码运行到最后导致windows10 企业版 LTSC 死机,为什么？

        • 王 茂南
          王 茂南
          2021年1月15日 下午5:47 B1
          回复

          @ 老学生 你需要看一下自己电脑的配置，我是使用 GPU 运行的。可以尝试把 batchsize 调小。

            • 王 茂南
              王 茂南
              2021年1月15日 下午5:48 B2
              回复

              @ 王 茂南 不过我感觉数据量不是很大，你是在训练的时候死机吗，是刚开始训练，还是训练了一会。

              • 老学生
                老学生
                2021年1月15日 下午6:57 B2
                回复

                @ 王 茂南 好的，我试试。

                • 老学生
                  老学生
                  2021年1月15日 下午7:20 B2
                  回复

                  @ 王 茂南 刚刚在调试状态运行了程序，结果如下：

                  \anaconda3\lib\site-packages\torch\nn\modules\loss.py:445: UserWarning: Using a target size (torch.Size([])) that is different to the input size (torch.Size([1, 1])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
                  return F.mse_loss(input, target, reduction=self.reduction)

                  程序运行到
                  Epoch:0510, MSE:0.021993393
                  ============

                  代码在’loss.backward()’ 处引发异常: bad allocation

                  Message=bad allocation
                  Source=F:\MsVsPython\Pytorch\一个初级例子代码\GRUtest\Prj\TrySimplGru\TrySimplGru.py
                  StackTrace:
                  File “F:\MsVsPython\Pytorch\一个初级例子代码\GRUtest\Prj\TrySimplGru\TrySimplGru.py”, line 236, in
                  loss.backward()

                  是不是那个警告有隐含的错误？我是初学者，不很懂，还请指点！

              • 老学生
                老学生
                2021年1月15日 下午6:52 2F
                回复

                好像是训练完成最后显示时死机的

                  • 王 茂南
                    王 茂南
                    2021年1月16日 下午10:35 B1
                    回复

                    @ 老学生 我看了 warning，是 loss 的 target size 和 input size 不同，我在我本地测试了一下，确实会有这个问题，但是不会影响。同时你可以通过 reshape 或者 view 来做改变 target 的大小，这样可以把 warning 去掉。

                    你可以去这个链接，Notebook 的 Github 链接，有一个 Time Series in PyTorch.ipynb 文件，看一下完整的代码。你可以尝试直接运行这个文件，看一下是否出错。（不过可能是 Pytorch 版本的问题，我的版本是 1.7）。

                    我看了一下之前写的代码，确实写得比较粗糙，batch size 都是 1，你可以自己调整一下。当时自己就是想做个测试，就没把代码写的比较完善。

                  • 老学生
                    老学生
                    2021年1月15日 下午6:55 3F
                    回复

                    从博文的结果看好像代码克服了LSTM时序预测平移延迟的现象，不过我现在没有运行到最后，也无法验证，请问你把结果图形放大后确实是这样理想吗？

                    • 老学生
                      老学生
                      2021年1月20日 下午4:23 4F
                      回复

                      我跑你的jupyter notebook版本，python=3.8.3,pytorch=1.7.1,win10 LTSC 1089,依然出错：

                      Epoch:0900, MSE:0.025476430
                      ============
                      —————————————————————————
                      RuntimeError Traceback (most recent call last)
                      in
                      23 # backward
                      24 loss = loss + criterion(output, j)
                      —> 25 loss.backward()
                      26 # optimize
                      27 optimizer.step()

                      C:\Anaconda\envs\torch\lib\site-packages\torch\tensor.py in backward(self, gradient, retain_graph, create_graph)
                      219 retain_graph=retain_graph,
                      220 create_graph=create_graph)
                      –> 221 torch.autograd.backward(self, gradient, retain_graph, create_graph)
                      222
                      223 def register_hook(self, hook):

                      C:\Anaconda\envs\torch\lib\site-packages\torch\autograd\__init__.py in backward(tensors, grad_tensors, retain_graph, create_graph, grad_variables)
                      128 retain_graph = create_graph
                      129
                      –> 130 Variable._execution_engine.run_backward(
                      131 tensors, grad_tensors_, retain_graph, create_graph,
                      132 allow_unreachable=True) # allow_unreachable flag

                      RuntimeError: bad allocation

                      • ghm
                        ghm
                        2021年3月18日 下午8:45 5F
                        回复

                        forward()里面已经有调用init_hidden()了，在每个batch里面似乎不用再写一遍model.hidden = model.init_hidden()了吧

                          • 王 茂南
                            王 茂南
                            2021年3月20日 下午12:42 B1
                            回复

                            @ ghm 嗯嗯，是的，只需要在 forward 里面写就可以了。