文章目录(Table of Contents)
简介
这一篇介绍关于高斯分布的均值和方差的推导的过程, 里面涉及的几个求积分的注意点还是可以看一下的, 也可以关注一下如何求期望.
下面所有的推导过程都是来自于下面的链接.
参考链接: how to derive the mean and variance of a Gaussian Random variable?
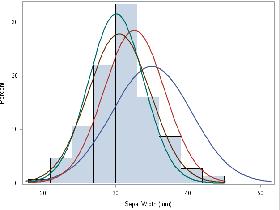
封面图片来自于: 统计学习 | 高斯分布
推导过程
一些预备知识
伽马函数:
百度百科对伽马函数的介绍: 伽玛函数
在实数域上伽玛函数定义为:
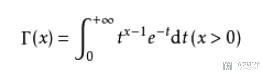
常用的积分:
具体的推导过程: 标准正态分布的积分怎么求?
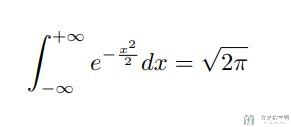
积分换元法:
参考链接: 换元积分法
看一个例子, 例子来自于上面的链接:
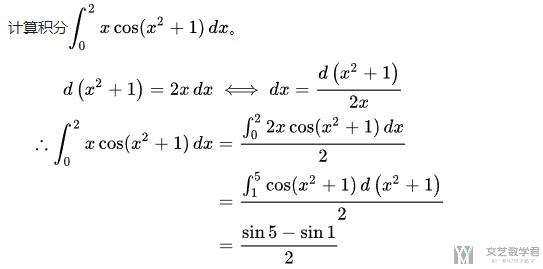
求期望
The Gaussian pdf is defined as:
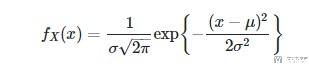
By definition of the mean we have:
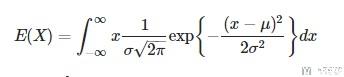
which using integral properties can be written as(这里使用了积分换元法, 将x'=x+u):
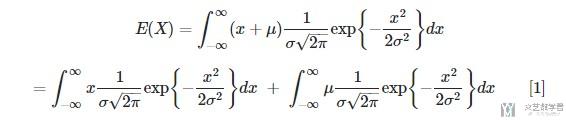
For the first integral, call it I1 we have using additivity(先对上式左边的进行化简):
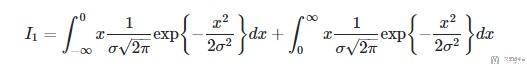
Swapping the integration limits in the first we have:
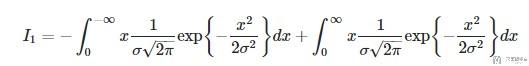
and using again integral properties we have(这里再使用一次积分换元法, 令x'=-x):
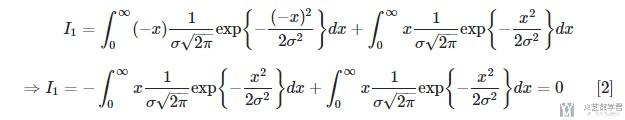
So we have that:
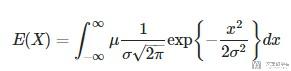
我们再使用一次积分换元法, 做下面的变化:
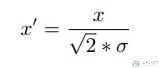
最后在结合上面的常用积分, 就可以求出高斯分布的均值了:
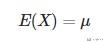
求方差
下面看一下求高斯分布方差的过程, 使用的一些技巧是和上面求均值是一样的, 这里就简单进行叙述.
We have:
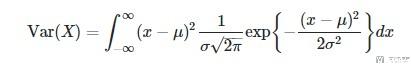
Applying the same tricks as before we have(最后是伽马函数, 参考上面关于伽马函数的介绍):
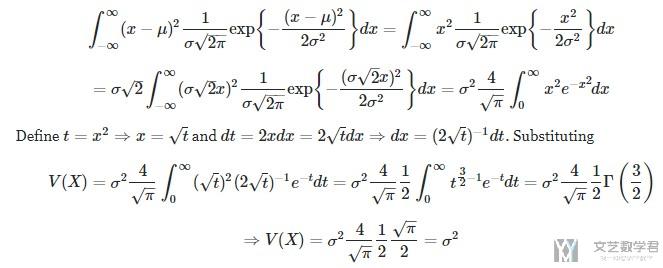
- 微信公众号
- 关注微信公众号
-

- QQ群
- 我们的QQ群号
-










评论