条件概率公式解释-一个例子

简介

这一篇会介绍关于条件概率公式, 贝叶斯公式和一个详细的例子计算.

之前其实我们有一篇类似的文章, 贝叶斯公式与全概率公式的应用-一道面试题. 但是那一篇没有把贝叶斯公式, 联合概率先讲明白, 就直接开始讲例子. 这一篇我们会讲的比较详细一些, 首先把这几个式子做一下简单的说明, 之后再给出一个例子. 我觉得这里的这个例子是十分好的.

一些数学基础

在讲应用之前, 我们先把这几个公式做一下简单的说明.

条件概率公式

首先我们说一下条件概率的公式, 当A=a发生的时候, B=b发生的概率, 我们可以写成下面的式子:

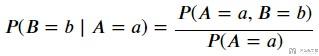
贝叶斯公式

当有了上面的条件概率的公式之后, 我们可以导出贝叶斯公式(Bayes' theorem). 根据乘法法则, 我们有以下的式子:

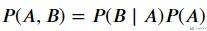
接着我们用这个式子对上面的条件概率公式进行化简, 可以得到贝叶斯公式.

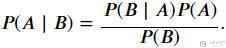
边缘概率密度

上面有了贝叶斯公式, 我们就可以进行一些推断, 例如计算B为某个值的时候, A此时的概率. 但是有的时候, 直接计算P(A), 或是直接计算P(B)是不方便的, 这个时候我们通过边缘概率的累加, 可以计算得到P(A)或是P(B), 例如下面的式子.

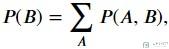
要计算P(A, B), 我们又可以通过P(A,B)=P(B|A)×P(A)来计算, 这样就是可以用P(A)来计算P(B).

一个小的应用

下面我们把上面讲到的公式, 实际应用一下. 这个例子是和之前一篇文章里的类似, 贝叶斯公式与全概率公式的应用-一道面试题., 但是这里会更进一步来进行说明.

假设现在有一个测试, 现在有以下几种可能性:

• 有1%的可能, 一个人是健康的, 但是被检测出来是不健康的;
• 如果是不健康的, 那么一定(100%)会被检测出来;

我们使用D1表示第一次的诊断结果, 其中1表示positive(不健康), 0表示negative(健康). H表示实际的情况, 也是1表示positive(不健康), 0表示negative(健康). 于是P(D1|H)会有以下的几种情况:

我们举一个例子, 稍微解释一下, P(D1=1|H=0)=0.01, 表示测试者身体是健康的, 但是被检测出来有问题的概率是0.01.

在人群总体中, 大部分的人是健康的, 不健康的大约是0.0015, 也就是P(H=1)=0.0015.

一次检测被误诊的概率

首先, 我们可以利用边缘概率密度, 来计算检测出来是不健康的概率, 也就是计算P(D1=1).

我们首先可以将P(D1=1)拆开考虑, 在检测为不健康的人里面有两类, 一类是本身就不健康(H=1), 一类是本身是健康的(H=0). 于是我们可以将P(D1=1)拆开考虑. 下面是整体的计算步骤.

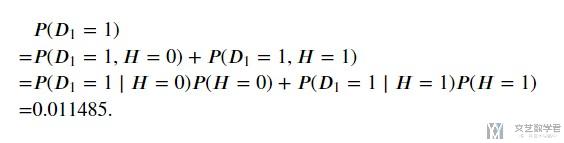
现在, 我们要求检测出来是不健康的, 实际上也是不健康的概率, 也就可以写成下面的式子, 这些值我们都已经有了, 直接代入计算即可, 也就是只有13%的可能性检测出来不健康, 实际也不健康:

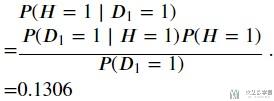
也就是说, 一次检测误诊的概率是(误诊指的是, 测试者实际是健康的, 但是检测结果却显示不健康)高达87%, 具体计算的过程如下所示.

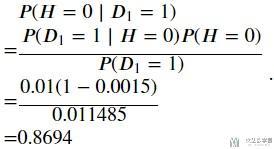
两次检测被误诊的概率

上面可以看到, 即使检测的准确率很高, 但是只进行一次检测被误诊的概率也是很高的. 那么做两次检测被误诊的概率呢.

首先看一下第二次检测的准确率. 因为第二次检测会换一种方法, 这种方法同样会有误诊的概率, 完整的对应如下表所示:

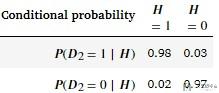
我们同样做一下简单的解释, P(D2=1|H=0)=0.03表示, 有3%的概率, 用户是健康的(H=0), 但是被检测出来是不健康的(D2=1).

同样, 我们需要计算此时被误诊的概率. 有如下的计算公式.

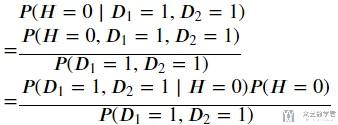
我们首先求P(D1=1, D2=1|H=0)的概率. 因为第一次测试和第二次测试是独立的, 所以我们可以进行如下的转换.

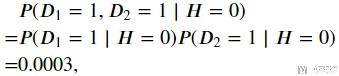
接着我们求P(D1=1, D2=1)的值.

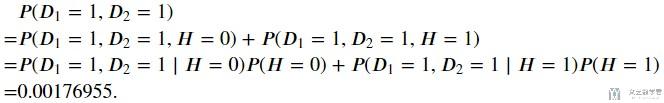
这样, 我们就可以求出被误诊的概率了, 也就是P(H=0|D1=1, D2=1).

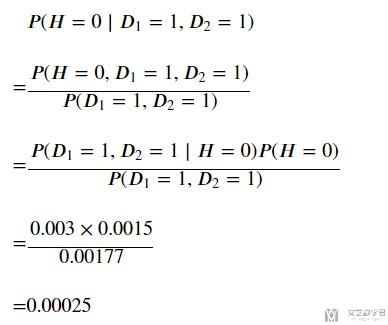
可以看到此时被误诊的概率就只有0.025%, 明显小了很多.