常见大数定律

这一篇文章是介绍常见的大数定律，一下所有的代码是基于Mathematica来实现的。

一、常见大数定律

1.伯努利大数定律

设na是n次独立重复试验中事件A发生的次数，p是事件A在每次试验中发生的概率，则对于任意整数ε>0，有：

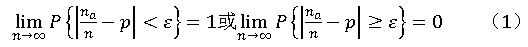
2.切比雪夫大数定律

设{Xn}为一列两两不相关的随机变量序列，若每个Xi的方差存在，且有共同的上界，即Var(Xi)≤c,i=1,2,…,则{Xn}服从大数定律，即满足（1）式。

3.马尔科夫大数定律

对随机变量序列{Xn}，若1/n^2 Var(∑(i=1--n)(X_i) )→0成立，则{Xn}服从大数定律，即满足（1）式。

4.辛钦大数定律

设{Xn}为一独立同分布的随机变量序列，若Xi的数学期望存在，则{Xn}服从大数定律，即满足（1）式。

二、Mathematica模拟

1.伯努利大数定律的模拟

模拟产生服从两点分布b（1，0.4）的随机数n个，计算事件A={产生的数值为1}的频率，与期望0.4相减观察误差，此处n取值分别为10，510，1010，1510，2010，2510。

t = {}; h = 0; p = 0; na = 0;

For[n = 10, n <= 3000, n += 500;
dist = RandomVariate[BinomialDistribution[1, 0.4], n];
na = Count[dist, x_ /; x > 0];
p = na/n;
h = p - 0.4;
t = Append[t, h]]

t
>>{-0.0176471, -0.0029703, -0.00529801, -0.0119403, 0.0131474, 0.00332226}

在n的取值越来越大时，误差值越小，但并非一致好，中间有反复，总体趋势是变小的

2.辛钦大数定律, 切比雪夫大数定律满足的例子模拟

模拟产生服从正态分布N（0，1）的随机数n个，计算随机变量序列dist的算术平均，观察其与期望0的差别，此处n取值分别为10，510，1010，1510，2010，2510。

t = {}; p = 0; na = 0;

For[n = 10, n <= 3000, n += 500;
dist = RandomVariate[NormalDistribution[0, 1], n];
na = Mean[dist];
t = Append[t, na]]

t
>>{-0.0276285, 0.00913863, 0.00817035, 0.0165267, 0.0102718, 0.00634342}

可以看出随着n的增加，均值越来越接近0。

3.蒙特卡洛法求定积分

例：设f(x)=0.3X^2，求f(x)在区间[0，1]上的积分值。

其标准值为0.166667，以下用两种方法分别模拟计算积分值。

随机投点法

设二维随机变量（X，Y）服从正方形{0≤x≤1，0≤y≤1}上的均匀分布，则X与Y分别都服从（0，1）上的均匀分布，记{Y≤f(X)}为事件A，则A发生的概率即为该定积分的值，可以多次重复试验，得到A出现的频率，由伯努利大数定律可知，此即可作为该定积分的估计值。

na = 0; h = 0; x1 = {}; y1 = {}; s = 0;

f[x_] = 0.5 x^2;

x1 = RandomVariate[UniformDistribution[{0, 1}], 10000];

y1 = RandomVariate[UniformDistribution[{0, 1}], 10000];

h = f[x1] - y1;

na = Count[h, x_ /; x > 0]
>>1619

s = N[na/10000, 6]
>>0.161900

平均值法

设X服从（0，1）上的均匀分布，则Y=f(X)的数学期望即为该定积分的值，由辛钦大数定律，可以用f(X)的观察值的平均去估计f(X)的数学期望的值，即可作为该定积分的估计值。

(*续接上部分代码*)

Mean[f[x1]]
>>0.166663

可见两种方法得到的值都和真值比较接近，扩大样本量可以得到更精确的结论，而在相同样本量下平均值法更为接近。