正态性检验

正态概率图

正态概率图，也就是P-P图（还有一种叫Q-Q图，区别在于纵轴不同）。正态概率图是一种很直接的正态性检验，它本质是一种坐标图，横轴为一系列取点值，纵坐标为相应的横坐标按正态分布函数值给出的值。具体处理步骤如下：

1. 列出给定的点x1,x2,...,xn
2. 将数据按从小到大的顺序排列得：x(1),x(2),...,x(n)
3. 对每一个i，计算修正概率（i-0.375）/（n+0.25），i=1,2,...,n
4. 将点( x(i) , (i-0.375)/（n+0.25）),i=1,2,...,n逐一点在正态概率图上
5. 观察上述n个点的分布，作如下判断：

• 若诸点在一条直线附近，则认为该批数据的总体是正态分布
• 如诸点明显不在一条直线附近，则认为该批数据的总体不是正态分布
• 说明：修正概率是为了弥补i=n时，概率值为1的缺陷。这里的修正概率值不是随便取的，一般有两个常见标准：i/(n+1)和（i-0.375）/（n+0.25）。国标GB/T 4882-2001推荐使用后者。

mathematica实现

data1 = RandomVariate[NormalDistribution[0, 2], 100];
data2 = RandomVariate[ExponentialDistribution[2], 100];
（*产生一个正态分布，一个指数分布分别做正态性检验对比结果*）
ProbabilityPlot[{data1, data2}, PlotLegends -> {Normal, Exponential},
PlotLabel -> "P-P Plot"]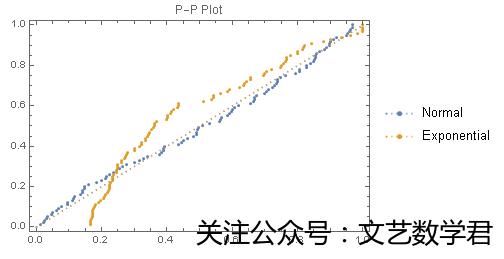

从图中可以看出，蓝色线的正态分布函数诸点几乎都在一条直线上，所以可以判定该数据是来自一正态分布的。

而桔色线有明显的偏斜，不成一条直线，所以可以断定该数据不是来自正态分布的，这也与实际数据符合。

该方法不用指定目标正态分布的具体特征值，检验的只是该数据是否是正态分布形式。

分布拟合检验

分布拟合检验即是验证一批数据是否满足某个具体分布，本质是一种假设检验，其原假设为总体分布满足目标分布。在这里把目标分布设定为正态分布，要求给出目标正态分布的具体均值和方差，是一种更加严谨的检验方法。

常见的分布拟合检验有Pearson χ2检验，Shapiro-Wilk检验，Watson U^2检验等，其具体公式比较复杂可以不用了解，使用方法同假设检验一样观察P值即可。

mathematica实现

DistributionFitTest[data1,
NormalDistribution[0, 2], {"TestDataTable", All}]
（*采用上述来自于正态分布的数据data1进行分布拟合检验*）

表中所列的名称即为mathematica可提供的假设检验，不同的检验结果略有差别，但是在90%的置信水平上都显示接受原假设，即认为该批数据来自于正态分布N（0，2）。 以上的检验都可以单独使用，比如Shapiro-Wilk检验，该检验在8≦n≦50时效果比较好，单独使用效果如下：

ShapiroWilkTest[data2]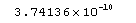

得出的是检验的P值，看出拒绝原假设，data2不满足正态分布，事实上data2是指数分布

• 说明

关于上面的皮尔森卡方检验，我感觉mathematica计算的值会有点问题，下面给一个例子的说明

data ={315.,108.,101.,32.};
dist ={312.75,104.25,104.25,34.75};
PearsonChiSquareTest[data,dist,"TestDataTable"]
Total[(data -dist)^2/dist] (*这个是定义的式子*)

其他可参考的检验方式

画出目标分布的正态密度曲线和所求数据的直方图进行直观观察，可以粗略的判断

mathematica实现

Show[Histogram[data1, NormalDistribution[0, 2], "ProbabilityDensity"],
Plot[PDF[NormalDistribution[0, 2], x], {x, -5, 5}]]
（*使用data1数据画直方图，并和N(0,2的密度曲线做对比)*）

从图中可以大致判断该分布是一正态分布，并且和N(0,2)较为重合，可以认为该数据满足N(0,2)，但把握度相比前一种方法来说不是很高，此时需要辅以偏度、峰度等其他可得到的统计特征来进一步说明。