方差分析

方差分析是Fisher首先提出的，简称为ANOVA。方差分析形式上是比较多个总体的均值是否相同，但本质上是探究变量之间的关系。

在方差分析中，所要检验的对象称为因素或因子，因素的不同表现称为水平或处理，每个因子水平下得到的样本数据称为观测值。由因子数不同，方差分析常分为单因素方差分析和双因素方差分析。

单因素方差分析

在问题中只考虑一个因子，则称为单因子试验，在只有一个因素的方差分析中，涉及两个变量：一个是分类型自变量，一个是数值型因变量。记单因子为A，设其有k个水平，记为A1,A2,...,Ak，在每一水平下考察的指标可以看成是一个总体，现有r个水平，故有k个总体，有如下假定：

(1)每一总体均为正态总体，记为N(μi , σi^2),i=1,2,...,k

(2)各总体的方差相同，记为σ1^2=σ2^2=...=σr^2=σ^2

(3)从每一总体中抽取的样本是相互独立的

下面详细介绍分析步骤

1.提出假设

方差分析是检验每个水平下的均值是否相同，即对如下的一个假设做检验：

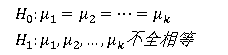
如果原假设成立，则称因子A的k个水平间没有显著差异，简称因子A不显著；反之当原假设不成立时，因子A的k个水平均值不全相同，此时称因子A的不同水平间有显著差异，简称因子A显著。

2.构造检验统计量

为构造检验统计量，在方差分析中，需要计算三个误差平方和，它们分别是总平方和、组间平方和（因素平方和）、组内平方和（误差平方和或残差平方和）。下面是三种误差平方和的计算。

总平方和（SST）：是全部观测与总均值的误差平方和，它反映了全部观测与总均值的之间的差异。其计算公式如下：

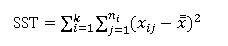
组间平方和（SSA）：是各组均值与总均值的误差平方和，反映了各样本均值之间的差异程度，因此又称为因素平方和。其计算公式如下：

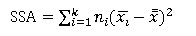
组内平方和（SSE）：是每个水平或组的各样本数据与其组均值的误差平方和，反映了每个样本各观测值的离散状况，该平方和反映了随机误差的大小。其计算公式如下：

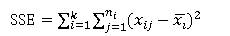
上述三个值有关系如：SST=SSA+SSE

同时注意到每组的观测值数量不一定相同（仔细看前面没有做这个要求），所以各误差平方和大小与观测值多少有关，为了消除观测值个数的影响，用各平方和除以它们对应的自由度，这一结果称为均方。这里主要比较的是组间均方和组内均方，所以只考虑SSA与SSE的均方，它们分别是：MSA=SSA/(k-1)、MSE=SSE/(n-k)

用上述MSA与MSE相比即可得到所需要的检验统计量F，当原假设为真时，二者的比值服从分子自由度为k-1、分母自由度为n-k的F分布，即：

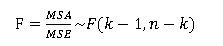
3.统计决策

代入数据计算统计量F，根据给定的显著性水平，找到对应的F分布数值，记为F（1-α）

若F>F(1-α)，则拒绝原假设，表明各水平均值之间的差异是显著的，也就是因子是显著的。

若F<F(1-α)，则不拒绝原假设，没有证据表明各水平均值之间的差异是显著的，此时不能证明因子是显著的。

mathematica实现

这里采用一个例题进行介绍。

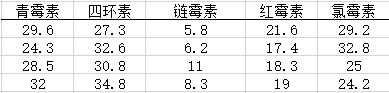
例：将抗生素注入人体会产生抗生素与血浆蛋白结合的现象，以致减少了药效，下表列出5种常用的抗生素注入到牛的体内时，抗生素与血浆蛋白结合的百分比。试在水平α=0.05下检验这些百分比的均值有无显著的差异。

解答：

Needs["ANOVA`"];(*使用发方差分析需要把此句写在前面*)
ANOVA[{{1, 29.6}, {1, 24.3}, {1, 28.5}, {1, 32.0},
{2, 27.3}, {2, 32.6}, {2, 30.8}, {2, 34.8},
{3, 5.8}, {3, 6.2}, {3, 11.0}, {3, 8.3},
{4, 21.6}, {4, 17.4}, {4, 18.3}, {4, 19.0},
{5, 29.2}, {5, 32.8}, {5, 25.0}, {5, 24.2}}]
(*每个括号内的数据填写方法是先写第几个因子，再顺序写下此因子下的观测值*)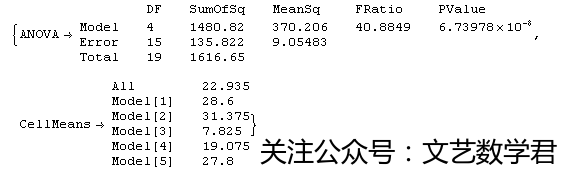

从输出结果可以看到，F值和相应的p值，简单而言比较p值即可，表明拒绝原假设，所以认为这5中抗生素的表现在给定的显著性水平下是有显著差别的。

双因素方差分析

当方差分析中涉及两个分类变量时，称为双因素方差分析，这里介绍无交互作用的双因素方差分析，无交互的意思是两个分类变量独立起作用。 由于有两个因素，因此在获取数据时，需要将一个安排在“行”是位置，称为行因素，另一个因素安排在“列”，称为列因素。设行因素A有k个水平，列因素B有r个水平，则共抽取kr个数据。

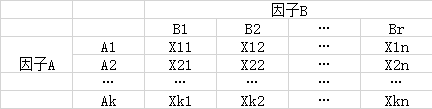
下面详细介绍分析步骤

1.提出假设

这里检验了两个因素的影响，所以提出如下假设：

2.构造检验统计量

和单因素房车分析中一样，这里也是将总平方和分解，但是把SST分解成行因素所产生的误差平方和SSR、列因素所产生的误差平方和SSC、除行因素和列因素之外的剩余因素所产生的误差平方和（即随机误差）SSE，其各自含义和单因素方差分析中提及分析思路的一样，具体公式如下：

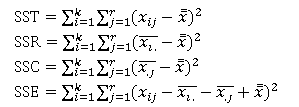
其中也存在关系：SST=SSR+SSC+SSE

同样也取各平方和的均方形式来构造检验统计量，此时行因素的均方为MSR=SSR/(k-1)，列因素的均方为MSC=SSC/(r-1)，随机误差项的均方为MSE=SSE/((k-1)(r-1))

检验行因素对因变量的影响是否显著，采用如下统计量：

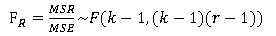
检验列因素对因变量的影响是否显著，采用如下统计量：

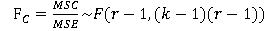
3.统计决策

方法同上，区别是双因素方差分析是对行因素和列因素分别比较。

mathematica实现

这里采用一个例题进行介绍。

例：有4个品牌的彩电在5个地区销售，为分析彩电的品牌和销售地区对销售量的影响，取得以下每个品牌在各地区的销售量数据（单位：台），如下表所示，试分析品牌和地区对彩电的销售量是否有显著影响（α=0.05）

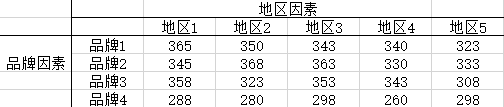
解答：

Needs["ANOVA`"];
ANOVA[{{1, 1, 365}, {1, 2, 350}, {1, 3, 343}, {1, 4, 340}, {1, 5, 323},
{2, 1, 345}, {2, 2, 368}, {2, 3, 363}, {2, 4, 330}, {2, 5, 333},
{3, 1, 358}, {3, 2, 323}, {3, 3, 353}, {3, 4, 343}, {3, 5, 308},
{4, 1, 288}, {4, 2, 280}, {4, 3, 298}, {4, 4, 260}, {4, 5,
298}}, {x, y}, {x, y}]
(*每个括号内的数据填写方法是先写第几个行因子，第几个列因子，再写下此定位下的观测值*)

图中的x和y分别代表行因素和列因素，其所在行对应各自的检验统计量值和p值，从输出结果可以看到，对行因素（即品牌因素）分析来看，拒绝原假设，认为这4种品牌的表现在给定的显著性水平下是有显著差别的，而对列因素（即地区因素）来看，接受原假设，认为这5个地区的表现在给定的显著性水平下是没有显著差别的。