常见的中心极限定理

1.林德伯格-莱维中心极限定理

设{Xn}是独立同分布的随机变量序列，且E(Xi )=μ,Var(Xi )=σ^2>0存在，若记

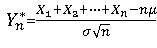
则对任意实数y，有：

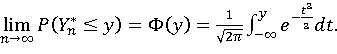
Mathematica模拟验证林德伯格-莱维中心极限定理

产生10000个（0，1）上的均匀分布的随机数并计算其标准化值，如此重复10000次，将得到的标准化值画出直方图，通过观察直方图图形，可以看到近似正态分布曲线，代码如下：

h = {};
sMean = 10000/2;
sVar = Sqrt[10000/12];
For[i = 1, i <= 9999, i++,
dist = RandomVariate[UniformDistribution[{0, 1}], 10000];
s = Total[dist];
y = (s - sMean)/sVar;
h = Append[h, y];
]
Histogram[h]

结果直方图：

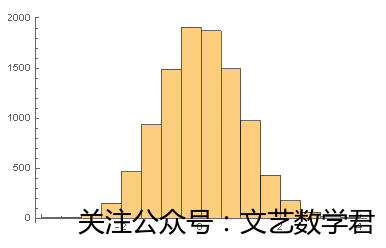
该例子可用于正态随机数的产生：先从（0，1）上的均匀分布产生12个随机数x1,x2,...,x12，再变换其为y=x1+x2+...+x12-6，则可以将y近似看成来自标准正态分布的一个随机数，如此重复进行。

2.棣莫佛-拉普拉斯中心极限定理

设n重伯努利试验中，事件A在每次试验中出现的概率为p(0<p<1)，记Sn为n次试验中事件A出现的次数，且记

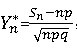
则对任意实数y，有：

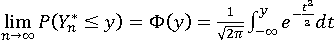
Mathematica模拟验证林德伯格-莱维中心极限定理

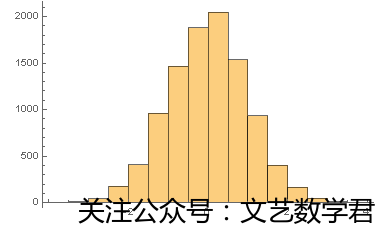
产生10000个服从p=0.4的两点分布的随机数并计算其标准化值，如此重复10000次，将得到的标准化值画出直方图，通过观察直方图图形，可以看到近似正态分布曲线，代码如下：

h = {};
For[i = 1, i <= 9999, i++,
dist = RandomVariate[BinomialDistribution[1, 0.4], 10000];
s = Count[dist, x_ /; x > 0];
y = (s - 4000)/48.9898;
h = Append[h, y];]
Histogram[h]

结果直方图：