正态总体参数的假设检验

摘要

介绍单个或两个正态分布的参数在不同情况下的假设检验问题及结论，并且通过mathematica分别实现对应条件下的假设检验

 

• 假设检验(Hypothesis Testing)是数理统计学中根据一定假设条件由样本推断总体的一种方法。

• 设检验具体步骤是：

 

1. 根据问题的需要对所研究的总体参数作某种假设，记作H0，则对立（大部分情况下）的假设记为H1
2. 根据参数选取合适的统计量，这个统计量的选取要使得在假设H0成立时，参数的分布为已知
3. 依据分布和检验水平构造拒绝域与接受域
4. 由实际的样本，计算出统计量的值，并根据预先给定的显著性水平进行检验，作出拒绝或接受假设H0的判断
5. 假设检验还可以通过计算p值来决定，p值是利用样本观测能够做出拒绝原假设的最小显著性水平，其中p值越大，则越倾向于接受原假设，p值越小，越倾向于拒绝原假设

• 假设检验通常有三种基本的原假设和备择假设组合：

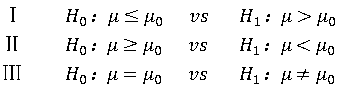
最常见的假设检验方法是关于正态分布的假设检验，以下详细介绍。

特别：下面有的知识与一些常见的抽样分布是重复的，即统计量的构造，那里有手写的公式的推导，可以点下面的链接去查看。 https://mathpretty.com/8842.html

一、单个正态总体均值的假设检验

此时原假设和备择假设组合采取上述形式

1.σ已知时

检验统计量：

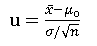
拒绝域：

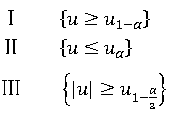
其中不等号右端u分位数为正态分布的分位数，左端为样本统计量，α为显著水平

Mathematica实现：

(Ⅲ型假设检验--这个比较常用)

data1 = RandomVariate[NormalDistribution[2, 3], 1000];
Mean[data1]
>>1.97409
（*查看数据均值，与2相近但有一点差距*）
(*已知方差为9，检验均值是否为2*)
ZTest[data1, 9, 2, "TestDataTable"]
(*ZTest函数依次填写：数据、已知方差、检验均值、显示方式（可不填）*)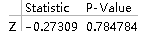

输出的结果分别为统计量值和P值，从P值可以看出接受原假设，认为均值为2

(*数据的光滑直方图*)
SmoothHistogram[data1]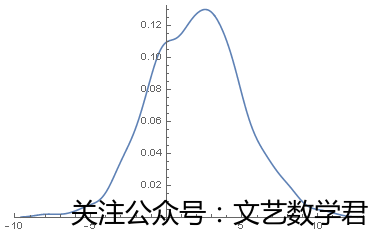

形状与正态分布较为符合，且从图中可以看出μ大约在2处

(Ⅱ型假设检验)

ZTest[data1, 9, 2, "TestDataTable", AlternativeHypothesis -> "Less"]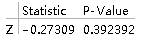

从p值看出接受原假设

(Ⅰ型假设检验)

ZTest[data1, 9, 2, "TestDataTable", AlternativeHypothesis -> "Greater"]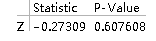

从p值看出接受原假设

 

2.σ未知时

 

检验统计量：

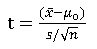
拒绝域：

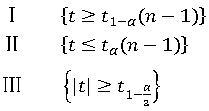
其中不等号右端t分位数为t分布的分位数，左端为样本统计量，α为显著水平

Mathematica实现：

(Ⅲ型假设检验)

TTest[data1, 2, "TestDataTable"]
(*TTest函数依次填写：数据、检验均值、显示方式（可不填）*)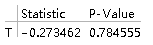

从p值看出接受原假设

(Ⅱ型假设检验)

Mean[data1]
>>1.97409
(*此处选择检验原假设为真实均值大于1.9*)
TTest[data1, 1.9, "TestDataTable", AlternativeHypothesis -> "Less"]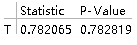

从p值看出接受原假设

(Ⅰ型假设检验)

(*此处选择检验原假设为真实均值小于1*)
TTest[data1, 1, "TestDataTable", AlternativeHypothesis -> "Greater"]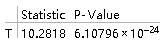

从p值看出拒绝原假设

 

二、两个正态总体均值差的假设检验

 

此时的三种常见的原假设和备择假设组合为：

 

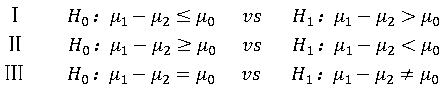
1.σ1，σ2已知时

 

检验统计量：

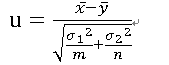
拒绝域：

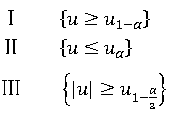
其中各符号含义同上

Mathematica实现：

(Ⅲ型假设检验)

data2 = RandomVariate[NormalDistribution[0, 2], 1000];
(*data1使用之前的数据，计算两组数据实际均值差*)
Mean[data1] - Mean[data2]
>>2.05895
(*在此设原假设为二者均值的差为0*)
ZTest[{data1, data2}, {9, 4}, 0, "TestDataTable"]
(*ZTest函数依次填写：两组数据、已知两组方差、检验均值差、显示方式（可不填）*)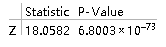

从p值看出拒绝原假设，认为两者均值差显著不等

(*尝试画出二者的光滑直方图曲线做直观比较*)
SmoothHistogram[{data1, data2}]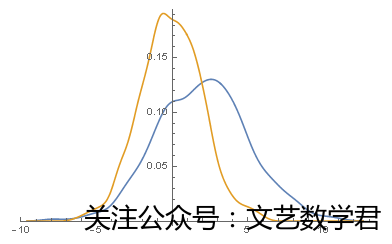

从图中可以看出，二者都是正态分布形式，并且二者的均值位置明显有差别，差别大小约为2

(Ⅱ型假设检验)

(*设原假设为两者均值差大于0.1*)
ZTest[{data1, data2}, {9, 4}, 0.1, "TestDataTable",
AlternativeHypothesis -> "Less"]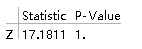

从p值可以看出接受原假设，两者均值差显著大于0.1

(Ⅰ型假设检验)

(*设原假设为两者均值差小于0*)
ZTest[{data1, data2}, {9, 4}, 0, "TestDataTable",
AlternativeHypothesis -> "Greater"]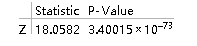

从p值可以看出显著拒绝原假设，两者均值差显著大于0

 

2.σ1=σ2但未知时

检验统计量：

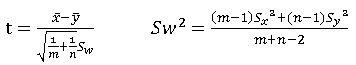
拒绝域：

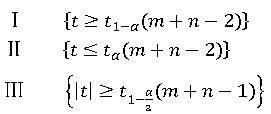
其中各符号含义同上

Mathemattica实现：

(Ⅲ型假设检验)

data3 = RandomVariate[NormalDistribution[0, 3], 1000];
(*产生和data1的方差相等的一批数据data3*)
Mean[data1] - Mean[data3]
>>2.00361
TTest[{data1, data3}, 2, "TestDataTable",
VerifyTestAssumptions -> "EqualVariance"]
(*TTest函数依次填写：两组数据、检验均值差、显示方式（可不填），方差相等假定*)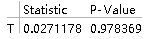

从p值可以看出接受原假设

(*画出两组数据的光滑直方图做直观观察，其中data3数据全体+2会使原始数据在图中向右移动，形状不变*)
SmoothHistogram[{data1, data3 + 2}]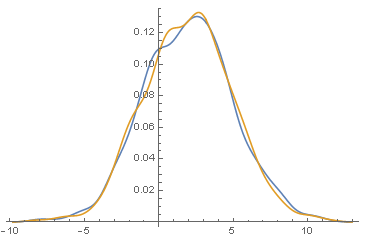

(Ⅱ型假设检验)

(*设原假设为两者均值差大于1.9*)
TTest[{data1, data3}, 1.9, "TestDataTable",
AlternativeHypothesis -> "Less",
VerifyTestAssumptions -> "EqualVariance"]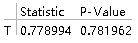

从p值可以看出接受原假设

(Ⅰ型假设检验)

(*设原假设为两者均值差小于2.1*)
TTest[{data1, data3}, 2.1, "TestDataTable",
AlternativeHypothesis -> "Greater",
VerifyTestAssumptions -> "EqualVariance"]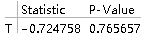

从p值可以看出接受原假设

 

3.成对数据检验

有时，当两个总体均值进行比较时，数据是成对出现的，这时候如果使用上面的两种方法得出的结论可能是不正确的，此时采用成对数据检验，其检验的原假设和备择假设形式同 二-2。

检验统计量：

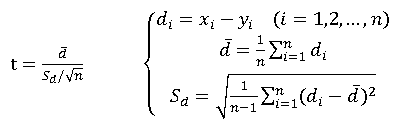
拒绝域：

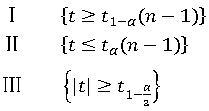其中各符号含义如上

Mathematica实现：

在此采用上述data1和data2，假设其为成对数据

(Ⅲ型假设检验)

PairedTTest[{data1, data2}, 2, "TestDataTable"]
(*PairedTTest函数依次填写：两组数据、检验均值差、显示方式（可不填）*)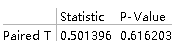

从p值可以看出接受原假设

(*对成对数据差做光滑直方图曲线，进行粗略观察*)
SmoothHistogram[data1 - data2]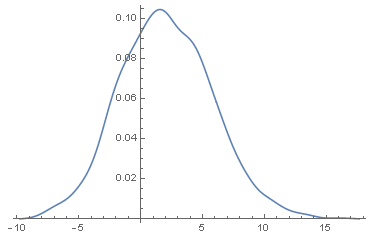

从图中可以看出，成对数据差的均值大约为2

(Ⅱ型假设检验)

(*设原假设为两者均值差大于1.9*)
PairedTTest[{data1, data2}, 1.9, "TestDataTable",
AlternativeHypothesis -> "Less"]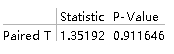

从p值可以看出接受原假设

(Ⅰ型假设检验)

(*设原假设为两者均值差小于2.1*)
PairedTTest[{data1, data2}, 2.1, "TestDataTable",
AlternativeHypothesis -> "Greater"]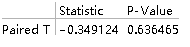

从p值可以看出接受原假设

 

三、单个正态总体方差的假设检验

 

此时常见的三种原假设和备择假设的组合为：

 

 

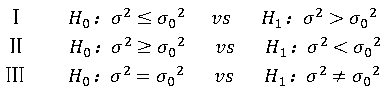
检验统计量：

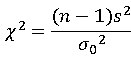
拒绝域：

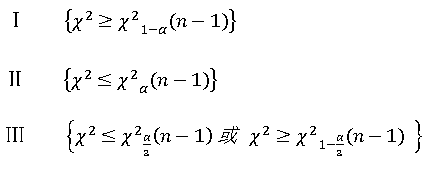
其中不等号右端χ2分位数为卡方分布的分位数，左端为样本统计量，α为显著水平

Mathematica实现：

(Ⅲ型假设检验)

VarianceTest[data1, 9, "TestDataTable"]
(*VarianceTest函数依次填写：数据、检验方差、显示方式（可不填）*)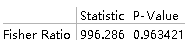

从p值可以看出接受原假设

(Ⅱ型假设检验)

(*设原假设为数据方差大于8*)
VarianceTest[data1, 8, "TestDataTable",
AlternativeHypothesis -> "Less"]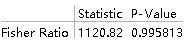

从p值可以看出接受原假设

(Ⅰ型假设检验)

(*设原假设为数据方差大于8*)
VarianceTest[data1, 10, "TestDataTable",
AlternativeHypothesis -> "Greater"]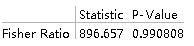

从p值可以看出接受原假设

 

四、两个正态总体方差比值的假设检验

此时常见的三种原假设和备择假设的组合为：

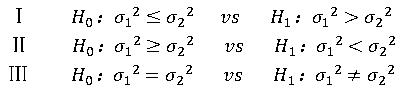
检验统计量：

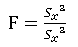
拒绝域：

其中不等号右端F分位数为F分布的分位数，左端为样本统计量，α为显著水平

Mathematica实现：

(Ⅲ型假设检验)

VarianceTest[{data1, data2}, 9/4, "TestDataTable"]
(*VarianceTest函数依次填写：两组数据、检验方差之比、显示方式（可不填）*)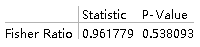

从p值可以看出接受原假设

(Ⅱ型假设检验)

(*设原假设为两组数据方差之比大于9/4*)
VarianceTest[{data1, data2}, 9/4, "TestDataTable",
AlternativeHypothesis -> "Less"]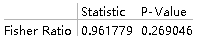

从p值可以看出接受原假设

(Ⅰ型假设检验)

(*设原假设为两组数据方差之比小于2.5*)
VarianceTest[{data1, data2}, 2.5, "TestDataTable",
AlternativeHypothesis -> "Greater"]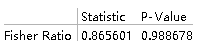

从p值可以看出接受原假设