卡方拟合优度检验

分类数据的卡方拟合优度检验

分类数据的拟合检验一般的情形为：根据某项指标，总体被分成r类：A1,A2,...,Ar，此时最关心的是各类元素在总体中所占的比率的假设（即检验问题）：

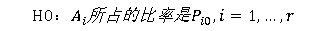
其中Pi0已知，且满足总和为1。

检验统计量：

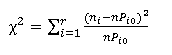
其中n是样本个数，ni是这n个样本中属于Ai的个数，当H0成立时，n个样本属于Ai类的“理论个数”（或说“期望个数”）为n·Pi0个，而实际观测到的值为ni。故当H0成立时，理论个数与实际个数应该相差不大，于是用上述统计量衡量此差异。之后计算相应p值得出结论。

以下采取一个经典的例子来进行mathematica的应用：

孟德尔按颜色和形状把豌豆分为四类：黄圆、绿圆、黄皱和绿皱。孟德尔根据遗传学原理推断这四类的比例为9：3：3：1，而试验得出的结果为，一共556个豌豆，其中四类的个数分别为315，108，101，32，那么这个结果能验证遗传学原理吗？

mathematica实现

data1 = {315, 108, 101, 32};(*实际个数*)
556*(9/16) // N(*理论中的黄圆个数*)
>>312.75
556*(3/16) // N(*理论中的绿圆个数*)
>>104.25
556*(3/16) // N(*理论中的黄皱个数*)
>>104.25
556*(1/16) // N(*理论中的绿皱个数*)
>>34.75
dist1 = {312.75, 104.25, 104.25, 34.75};(*理论个数*)
(*原假设是data和dist来自同一分布*)
PearsonChiSquareTest[data1, dist1, "TestDataTable"]
(*皮尔逊卡方检验*)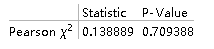

从P值可以得知接受原假设，即认为这四类的比例为9：3：3：1，孟德尔的遗传学原理得到了验证。

注：mathematica中的PearsonChiSquareTest所使用的计算过程和上述理论中介绍的有所不同，虽然最终判断结果一样，但相应的统计量值和P值与理论公式得到的不同，这里需要参考使用。

分布的卡方拟合优度检验

假设x1,x2,...,xn是来自总体F(x)的样本。

假设检验问题：

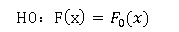
其中F0(x)可以是一个完全已知的分布，也可以是一个仅依赖于有限个实参数且分布形式已知的分布函数（此时的未知参数要使用最大似然估计来得到），称其为理论分布。当样本量较大时，可以采用卡方拟合优度检验来解决此类问题，matheamatica里面有可用于此类检验的函数。

mathematica实现

data2 = RandomVariate[PoissonDistribution[3], 200];
(*用泊松分布产生一组样本数据*)
Mean[data2] // N
>>3.095
(*是均值也是其最大似然估计，在缺少分布参数时可以由此来估计*)
PearsonChiSquareTest[data2, PoissonDistribution[3], "TestDataTable"]
(*用皮尔逊卡方检验来检验这组样本数据是否来自参数为3的泊松分布*)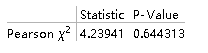

从结果的p值可以看出这组数据符合参数为3的泊松分布。

data3 = RandomVariate[NormalDistribution[2, 3], 100];
(*用正态分布产生一组样本数据*)
H = PearsonChiSquareTest[data3, NormalDistribution[2, 3], "HypothesisTestData"];
H["TestDataTable"]
H["TestConclusion"]
>> The null hypothesis that the data is distributed according to the NormalDistribution[2,3] is not rejected at the 5 percent level based on the Pearson X^2 test.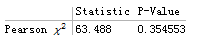

从结果的p值可以看出这组数据符合参数为2和9的正态分布。