文章目录(Table of Contents)
简介
在这里我们想结合实际的例子,来计算一下 CrossEntropyLoss 是如何计算的。同时也可以再强化一下交叉熵的计算。
关于交叉熵的一些推导性的内容,可以参考链接:
关于详细的 notebook, 可以在 GitHub 进行查看, PyTorch交叉熵介绍(CrossEntropy介绍)
CrossEntropyLoss 的理解
因为 CrossEntropyLoss 是由 LogSoftmax 和 NLLLoss 这两个类结合而来的,所以我们先来介绍一下这两个类的用法。最后再看一下 CrossEntropyLoss 的一个整体的计算流程。
LogSoftmax 的介绍
关于 LogSoftmax 所作的操作, 即先进行 Softmax,再对 Softmax 的结果求对数.
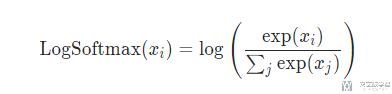
我们下面看一个具体的例子, 我们的输入是 (1,1,1,1),那么 LogSoftmax 就是进行如下的操作:
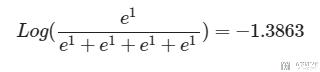
拆开来, 就是分为两步, 首先计算 Softmax,最后对结果求 Log:
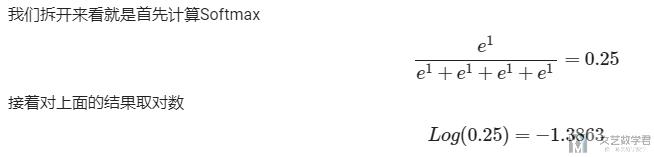
我们看一下使用 PyTorch 的计算结果,可以看到和上面我们自己计算是一样的:
- ll = nn.LogSoftmax()
- input = torch.tensor([1.0,1.0,1.0,1.0])
- output = ll(input)
- print(output)
- >> tensor([-1.3863, -1.3863, -1.3863, -1.3863])
NLLLoss的介绍
在说明文档中, NLLLoss计算方式如下, 就是使用predict与label进行相乘.
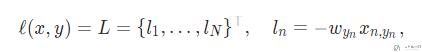
我们还是看一个下面的例子.
- loss = nn.NLLLoss()
- input = torch.tensor([[0.2, 0.3, 0.5]])
- target = torch.tensor([2]).long()
- output = loss(input, target)
- print(output)
- >> tensor(-0.5000)
上面的例子中, target为2, 也就是表示one-hot表示为(0,0,1), 于是NLLLoss的计算如下所示.
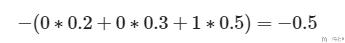
Pytorch使用LogSoftmax的原因
那么, 为什么在实际的使用过程中, 会将使用LogSoftmax, 而不是首先进行softmax, 再进行crossEntropy的计算呢. 这是因为在计算softmax的时候, 因为要计算指数, 所以很可能出现nan的情况. 又因为在分类问题里面, 最后使用CrossEntropy的时候需要进行log运算, 如果将Log运算和Softmax结合在一起, 可以避免这个问题.
下面是一个简单的化简步骤. 我们本来是要计算exp(o)的, 化简之后只需要计算o即可.
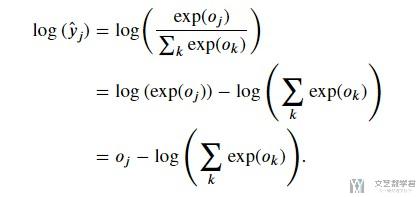
CrossEntropyLoss的介绍
介绍完上面两个部分, 我们就可以介绍在PyTorch中的交叉熵了. 但是我们首先看一下交叉熵是如何进行计算的.
交叉熵计算
首先我们先不管Pytorch中是如何实现交叉熵的, 我们先自己来看一下交叉熵是如何计算的. 交叉熵的计算公式如下所示:
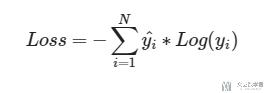
其中:

那么, 当现在的输出的概率是(1/4, 1/4, 1/4, 1/4)的时候, target是(0, 0, 0, 1)的时候, 此时的交叉熵计算结果就是1.3863.
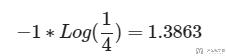
关于PyTorch中的CrossEntropyLoss
下面我们看一下PyTorch中CrossEntropy是如何计算的. 前面说了, CrossEntropy是LogSoftmax和NLLLoss的结合. (下面我直接截个图, 里面公式比较多, 一个一个讲比较麻烦, 原始的可以查看GitHub链接, PyTorch交叉熵介绍(CrossEntropy介绍))
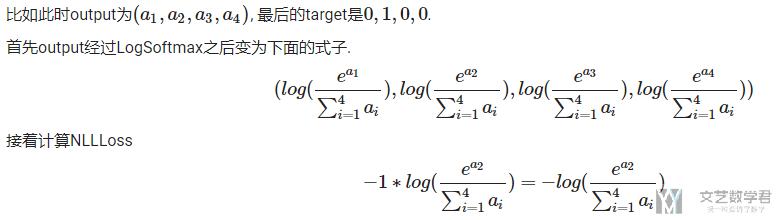
这个结果是和上面交叉熵的定义是一样的. 我们可以想象成在LogSoftmax中, 我们不仅将原来的output转换为了概率值, 还求了log, 最后只需要和target相乘即可.
需要注意的是, 这里NLLLoss虽说叫做(negative log likelihood loss), 但是他并没有在计算log, log的运算时放在了上面的LogSoftmax里面进行的.
下面有一个例子:
- loss = nn.NLLLoss()
- Y = torch.tensor([2, 1, 0])
- data = torch.tensor(
- [[0.3, 0.3, 0.4],
- [0.3, 0.4, 0.3],
- [0.1, 0.2, 0.7]])
- loss(data, Y)
- # >> tensor(-0.3000)
这里输出的-0.3就是-(0.4+0.4+0.1)/3=-0.3.
CrossEntropyLoss实验验证
接下来我们实际操作一下, 来验证一下上面的结论. 我们只需要将CrossEntropyLoss的input设置为(1,1,1,1), 这样经过softmax之后的概率就(1/4,1/4,1/4,1/4), 所以这里计算得到的交叉熵应该是1.3863.
- loss = nn.CrossEntropyLoss()
- input = torch.tensor([[1, 1, 1.0, 1]])
- target = torch.tensor([2]).long()
- output = loss(input, target)
- print(output)
- >> tensor(1.3863)
同时, 我们还知道
- 当预测的概率为(1,0,0), 实际值(target)是(1,0,0)的时候, 交叉熵是接近0的.
- 当预测的概率为(0,0,1), 实际值(target)是(1,0,0)的时候, 交叉熵是接近正无穷的.
- # 预测和实际很接近
- loss = nn.CrossEntropyLoss()
- input = torch.tensor([[0, 0, 100.0]])
- target = torch.tensor([2]).long()
- output = loss(input, target)
- print(output)
- >> tensor(0.)
当预测结果和实际相差较远的时候.
- # 预测和实际差很远
- loss = nn.CrossEntropyLoss()
- input = torch.tensor([[100.0, 0, 0]])
- target = torch.tensor([2]).long()
- output = loss(input, target)
- print(output)
- >> tensor(100.)
一些可能出现的问题
注意在Pytorch中, CrossEntropyLoss是包含了softmax的内容的. 所以如果我们损失函数使用了CrossEntropyLoss, 那么网络的最后一层就使用linear就可以, output就是要分类的个数.
有的时候会出现如下的报错,
- CrossEntropy in Pytorch getting Target 1 out of bounds
这是因为使用CrossEntropyLoss, 最后网络的输出的维度与分类个数是相同的. 例如2分类, 不能只输出一个0-1之间的值, 应该有两个数, 之后CrossEntropyLoss会在里面计算softmax.
也就是下面的解释(下面是出现上面报错的原因):
nn.CrossEntropyLoss is used for a multi-class classification, while your model outputs the logits for a single class. (出现报错的原因, 在一个二分类的问题中)
If you are dealing with a binary classification, you could use nn.BCEWithLogitsLoss, or output two logits and keep nn.CrossEntropyLoss. (使用CrossEntropyLoss的时候, 网络的output就是要有2, linear的output的维度是2)
参考资料, CrossEntropy in Pytorch getting Target 1 out of bounds
- 微信公众号
- 关注微信公众号
-

- QQ群
- 我们的QQ群号
-













评论