Pytorch入门教程02-梯度的求解

王 茂南
王 茂南
王 茂南
3081
文章
75
评论
2020年10月2日07:47:04
评论3 4015字阅读13分23秒
摘要这一篇介绍一下使用Pytorch来求解梯度. 会给出一个例子, 我们自己推导一遍梯度的求导, 然后与Pytorch的autograd的结果比较.

简介

在神经网络中, 我们需要计算梯度, 使用梯度下降(或上升)来完成参数的更新. 所以, 在这一部分, 我们主要介绍梯度的计算, 以及Pytorch中计算梯度的相关内容.

之前我们写过一个总体的版本, Backpropagation(反向传播)方法介绍. 在这一篇, 我们拆开来一部分一部分详细来说明.

这一部分主要内容包括:

  • 梯度的简单介绍
  • 梯度的计算
    • 一个简单的例子
    • 一个稍微复杂的例子
    • 计算梯度的时候增加权重
  • 停止梯度计算
  • 梯度清空, zero_grad()的介绍

 

梯度的介绍

在一元函数中, 某点的梯度表示的就是某点的导数. 但是在多元函数中某点的梯度表示的是, 由每个自变量所对应的偏导值所组成的向量. 例如f(x,y,z)的梯度就是一个三维的向量, 如下所示:

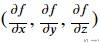
Pytorch入门教程02-梯度的求解

梯度的方向就是函数值上升最快的方向.

梯度的计算

在Pytorch中, 我们可以使用torch.autograd.backward()来自动计算变量的梯度, 该函数会对指定的变量进行偏导的求取.

同时, 为了区分函数中哪些变量需要求偏导, 哪些不需要求偏导, 在定义张量(tensor)的时候, 我们会加上requires_grad=True用来表示该变量可以可以求偏导数.

梯度计算简单例子

下面我们来看一个简单的例子, 定义x, y, z三个变量, 其中x是需要计算梯度的.

  1. x = torch.tensor([1.0], requires_grad=True)
  2. y = torch.tensor([2.0])
  3. z = torch.tensor([2.0])
  4. # 定义运算
  5. f1 = 2*x+y # 2*1+2=4
  6. print(f1)
  7. # tensor([4.], grad_fn=<AddBackward0>)
  8. print(f1.grad_fn)
  9. # <AddBackward0 object at 0x7fcc97180790>
  11. f2 = y+z # 2+2=4
  12. print(f2)
  13. # tensor([4.])
  14. print(f2.grad_fn)
  15. # None

于是可以看到, 因为x是有梯度的, f1是通过x计算得到的, 所以f1也是可以求导的. 因为这里f1=2*x+y, 所以df1/dx=2. 我们验证一下结果.

我们利用f1.backward()求f1的梯度, 接着使用x.grad(也就是df1/dx的值)来打印偏导数.

  1. # 求梯度
  2. f1.backward()
  3. print(x.grad)  # df1/dx
  4. # >> tensor([2.])
  5. print(y.grad)
  6. # >> None

可以看到因为在上面定义x的时候, 是有requires_grad=True, 但是定义y的时候是没有的, 所以这里查看偏导数的时候, df1/dx=2, 但是df1/dy是没有的的, 是None.

 

一个稍微复杂的梯度计算例子

接着我们稍微看一个稍微有点复杂的例子, 我们看一个复合函数z:

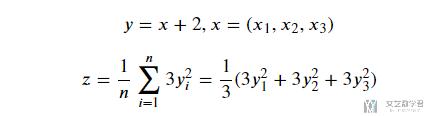
Pytorch入门教程02-梯度的求解

我们这里想要求dz/dx, 于是我们以dz/dx1来作为例子进行说明.

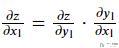
Pytorch入门教程02-梯度的求解

于是, 这里就分为两部分, 分别是求dz/dy1和dy1/dx1. 首先是计算dz/dy1, 结果如下所示:

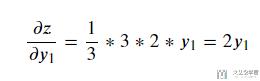
Pytorch入门教程02-梯度的求解

接着是计算dy1/dx1:

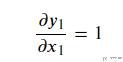
Pytorch入门教程02-梯度的求解

于是最终的偏导数如下所示:

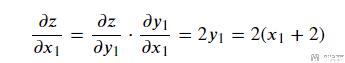
Pytorch入门教程02-梯度的求解

接下来我们使用Pytorch来做一下测试.

  1. x = torch.randn(3, requires_grad=True)  # x 中存了三个变量 x1,x2,x3
  2. y = x + 2
  3. z = y * y * 3
  4. z = z.mean()
  6. # 求导
  7. z.backward()
  8. print(x.grad)  # dz/dx
  10. # 比较直接计算的结果
  11. print(2*(x+2))

最终手动求导的结果, 与直接计算的结果是一样的. 最终结果如下图所示.

Pytorch入门教程02-梯度的求解

 

原始梯度加权

在使用torch.autograd.backward求解变量的偏导数的时候, 我们是可以给原偏导数进行不同的加权. 如果使用函数 k.backward(p), 则得到的的变量x.grad 的值为:

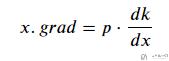
Pytorch入门教程02-梯度的求解

下面看一个例子. z=(2^11)*x, 这里x包含x1,x2,x3, 我们对x1, x2, x3的偏导给不同的权重.

  1. x = torch.ones(3, requires_grad=True)
  3. z = 2**11*x # 也就是2^11=2048
  5. print(z)
  6. # >> tensor([2048., 2048., 2048.], grad_fn=<MulBackward0>)
  8. p = torch.tensor([0.1, 1.0, 0.0001], dtype=torch.float32) # 求偏导数的时候, 给不同的权重
  9. z.backward(p)
  10. print(x.grad)
  11. # >> tensor([2.0480e+02, 2.0480e+03, 2.0480e-01])

 

停止梯度计算

如果我们不需要某些张量的梯度计算, 我们就可以使用下面三种方法来停止某个张量(tensor)的梯度的计算, 这三种方法分别是:
  • x.requires_grad_(False)
  • x.detach()
  • with torch.no_grad():

 

requires_grad

requires_grad可以直接修改张量x的属性, 如下面的例子.

  1. a = torch.ones(2, 2, requires_grad=True)
  2. b = ((a * 3) / (a + 1)).sum()
  3. b.backward()
  4. print(b.grad_fn)  # 此时可偏导，求取梯度的函数存在
  5. # >> <SumBackward0 object at 0x7fcc960f4650>
  6. print(a.grad)
  7. """
  8. tensor([[0.7500, 0.7500],
  9.         [0.7500, 0.7500]])
  10. """
  12. a.requires_grad_(False)
  13. b = ((a * 3) / (a + 1)).sum()
  14. print(b.grad_fn)  # 此时不可偏导了，求取梯度的函数不存在了
  15. # >> None
  16. # b.backward() # 此时不能求导

如果去掉最后一行的注释, 会出现如下的报错, 这是因为将requires_grad设置为False的原因.

  1. RuntimeError: element 0 of tensors does not require grad and does not have a grad_fn

 

detach

detach是将x中提取其中的内容, 但是新的张量不能计算梯度.

  1. a = torch.randn(2, 2, requires_grad=True)
  2. b = a.detach()
  3. print(a.requires_grad)
  4. # >> True
  5. print(b.requires_grad)
  6. # >> False

 

with torch.no_grad

这个通常是用在测试集上面的, 测试的时候是不需要计算梯度的. 在这里面都是不需要计算梯度的.

  1. a = torch.ones(2, 2, requires_grad=True)
  2. print((a**2).requires_grad)
  3. # >> True
  4. with torch.no_grad():  # 该作用域下定义的都是不进行梯度计算的张量
  5.     print((a**2).requires_grad)
  6.     # >> False

 

梯度清空

梯度清空介绍

在pytorch中, 如果多次使用torch.autograd.backward, 得到的梯度会进行累加. 下面看一个例子.

Pytorch入门教程02-梯度的求解

我们在Pytorch中实现上面的内容, 但是注意我们进行两次求导, 可以看到dz/dx的导数是4, 这是把dy/dx的也累加进去了. 这是因为所有对x的偏导数, 都会被存入x.grad中.

  1. x = torch.ones(4, requires_grad=True)
  2. y = (2*x+1).sum()
  3. z = (2*x).sum()
  4. y.backward()
  5. print("第一次偏导：", x.grad)  # dy/dx=2
  6. # >> 第一次偏导： tensor([2., 2., 2., 2.])
  8. z.backward()
  9. print("第二次偏导：", x.grad)  # dy/dx+dz/dx
  10. # >> 第二次偏导： tensor([4., 4., 4., 4.])

为了避免这个问题, 通常我们在计算梯度之后, 都需要清空梯度. 也就是会使用x.grad.zero_()来进行清空梯度.

比如还是上面的例子, 我们在第一次求梯度之后, 清空一次x的梯度, 再求. 可以看到此时第二次偏导的结果是2, 和我们上面自己计算得到的内容是一样的.

  1. x = torch.ones(4, requires_grad=True)
  2. y = (2*x+1).sum()
  3. z = (2*x).sum()
  4. y.backward()
  5. print("第一次偏导：", x.grad)  # dy/dx
  6. # >> 第一次偏导： tensor([2., 2., 2., 2.])
  8. x.grad.zero_() # 清空x的梯度
  10. z.backward()
  11. print("第二次偏导：", x.grad)  # dz/dx
  12. # >> 第二次偏导： tensor([2., 2., 2., 2.])

zero_grad()介绍

梯度清空是非常重要的, 因为之后模型训练的时候, 每一轮都会计算梯度, 如果一直在累加, 后面梯度就会越来越大. 因此我们需要在每一轮结束清空梯度.

除了张量中存在梯度清空函数, 优化器中也存在这样的函数: zero_grad(), 所以在实际写的时候, 我们通常在训练步骤里是这样写的.

  1. # 前向传播
  2. out = network(batch_x)
  3. loss = loss_fn(out, batch_y) # 计算损失
  4. # 梯度清零
  5. optimiser.zero_grad()
  6. # 反向传播
  7. loss.backward()
  8. optimiser.step() # 随机梯度下降

 

  • 微信公众号
  • 关注微信公众号
  • weinxin
  • QQ群
  • 我们的QQ群号
  • weinxin
王 茂南
  • 本文由 发表于 2020年10月2日07:47:04
  • 转载请务必保留本文链接：https://mathpretty.com/12498.html
匿名

发表评论

匿名网友 填写信息

:?: :razz: :sad: :evil: :!: :smile: :oops: :grin: :eek: :shock: :???: :cool: :lol: :mad: :twisted: :roll: :wink: :idea: :arrow: :neutral: :cry: :mrgreen: