文章目录(Table of Contents)
简介
之前写过一份正向传播与反向传播, 链接为: Backpropagation(反向传播)方法介绍. 当时写的时候往里面融合了太多的东西, 包括整个流程, 这里我们将其拆开, 单独说一下正向传播与反向传播.
这一部分主要介绍两个大部分:
- 正向传播
- 反向传播
下面是两个在反向传播的时候可能用到的数学知识, 放在这里.
Sigmoid函数导数
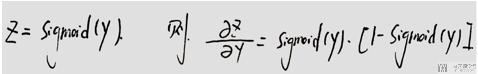
正向传播
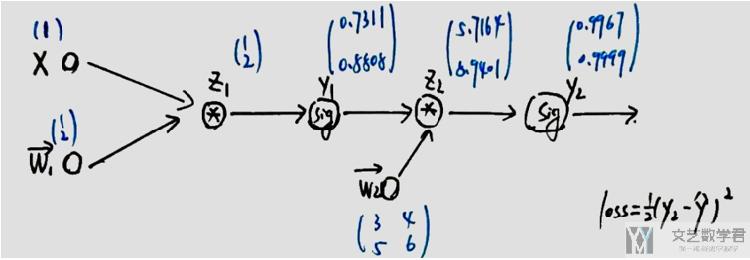
我们知道, 神经网络就是一个复合函数. 正向传播其实就是输入, 通过神经网络, 得到输出的一个过程. 例如下面的例子, 此时:
- 输入x=1
- 其中有权重参数w1和w2, 初始化如下图所示
- 整个运算过程为, y_pre = sigmoid(sigmoid(w1*x)*w2), loss = (y_pre-y_real)^2
我们把上面的过程使用Pytorch复现一下. 首先定义上面的整个运算过程.
- def forwrad(x, y, w1, w2):
- # 其中 x,y 为输入数据,w为该函数所需要的参数
- z_1 = torch.mm(w1, x)
- y_1 = torch.sigmoid(z_1)
- z_2 = torch.mm(w2, y_1)
- y_2 = torch.sigmoid(z_2)
- loss = 1/2*(((y_2 - y)**2).sum())
- return loss, z_1, y_1, z_2, y_2
接着我们初始化输入, 和上面的系数w1和w2. 最后的target是(1,0).
- # 测试代码
- x = torch.tensor([[1.0]])
- y = torch.tensor([[1.0], [0.0]])
- w1 = torch.tensor([[1.0], [2.0]], requires_grad=True)
- w2 = torch.tensor([[3.0, 4.0], [5.0, 6.0]], requires_grad=True)
- loss, z_1, y_1, z_2, y_2 = forwrad(x, y, w1, w2)
- print(loss)
- """
- y1的值: tensor([[0.7311],
- [0.8808]], grad_fn=<SigmoidBackward>)
- y2的值: tensor([[0.9967],
- [0.9999]], grad_fn=<SigmoidBackward>)
- loss的值: tensor(0.4999, grad_fn=<MulBackward0>)
- """
于是在正向传播的过程中, 会计算得到中间变量y1和y2, 和得到最终的loss, loss为0.4999.
反向传播
反向传播是为了计算输出与参数(上面的w1和w2)之间的梯度关系. 在上面的计算中, 我们的系数不能保证最终的output与target是一样的, 也就会产生loss.
为了减小loss, 我们会使用梯度下降法. 要使用梯度下降法, 就需要用到各个系数的偏导数. 于是反向传播就是用来计算系数的偏导数的.
对于上面的问题, 我们首先手动推导一下w1和w2的梯度, 首先是w2的梯度(这里会用到上面的数学基础内容).
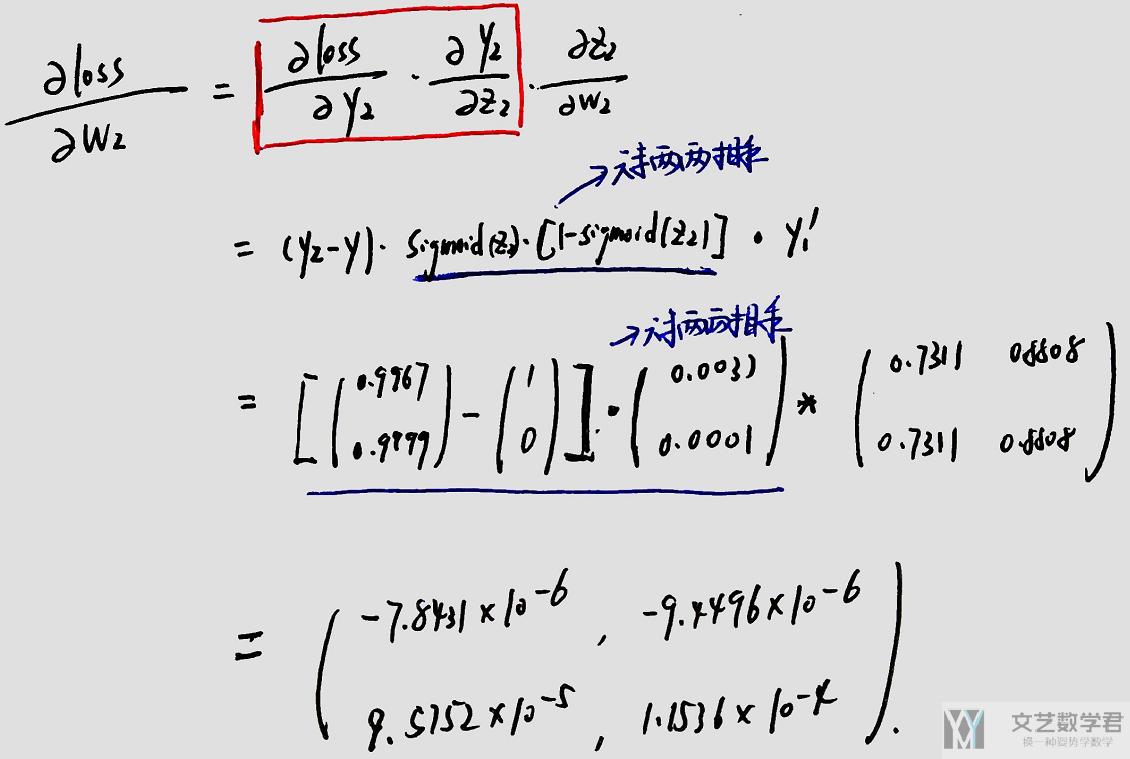
接着是计算w1的梯度, 在计算w1梯度的时候, 上面红色框内的部分是可以复用的.
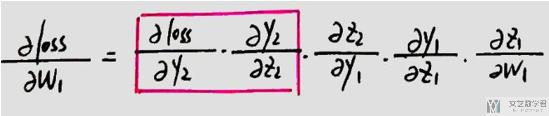
在pytorch中, 我们可以直接使用loss.backward() 进行反向传播, 计算出系数的偏导数.
- loss.backward() # 反向传播,计算梯度
- print('w1的梯度, {}'.format(w1.grad))
- print('w2的梯度, {}'.format(w2.grad))
- """
- w1的梯度, tensor([[1.2243e-04],
- [7.8005e-05]])
- w2的梯度, tensor([[-7.8431e-06, -9.4496e-06],
- [ 9.5752e-05, 1.1536e-04]])
- """
这里通过Pytorch计算得到的梯度, 和上面自己推导得到的梯度值是一样的.
- 微信公众号
- 关注微信公众号
-

- QQ群
- 我们的QQ群号
-













评论