文章目录(Table of Contents)
简介
上一篇我们计算得到了各个系数(w1和w2)的梯度, 这一篇我们介绍梯度下降法, 来优化这些系数. 这一篇主要有以下几个部分:
- 梯度下降法的简单介绍;
- 手动实现梯度下降法;
- 使用Pytroch自动实现梯度下降, 结合backward实现.
这一部分的代码已经上传github: 梯度下降法示例
梯度下降介绍
由于梯度表示的是函数上升最快的方向, 因此梯度的反方向也应该是函数下降最快的方向. 我们每次到了一个新的位置, 就会就计算该位置的梯度, 找到下一步下降最快的方向. 整个过程如下所示, 我们每次更新一小步, 逐渐找到最优点的位置.
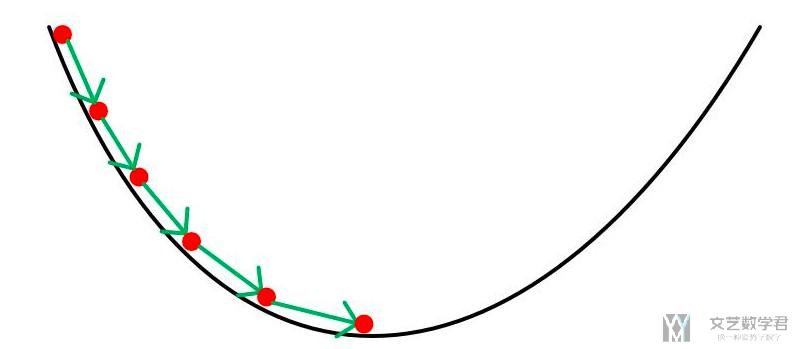
若J是损失函数, 则根据梯度和当前位置更新下一次所在位置的数学表达式如下:
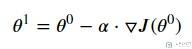
我们反复进行迭代, 就可以找到J的最优的系数theta.
人工实现梯度下降法
生成测试数据
我们这里用一个一元线性回归来作为例子. 首先我们生成测试数据. X和Y关系是: Y=2X.
- # 定义数据集合
- X = np.arange(0,10,0.1, dtype=np.float32)
- Y = 2*X + 2*np.random.random(100)
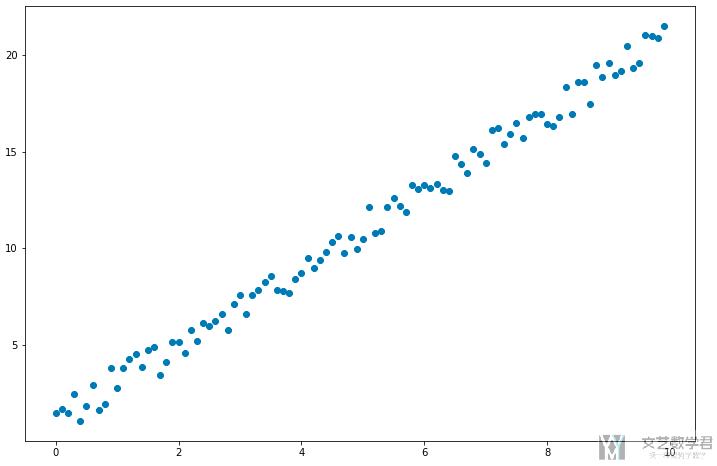
我们对数据进行可视化.
- # 可视化数据集
- fig = plt.figure(figsize=(12,8))
- ax = fig.add_subplot(1,1,1)
- ax.scatter(X,Y)
- fig.show()
可视化结果如下所示:
定义损失函数
我们希望找出一个W, 使得W*X的值与Y越接近越好. 那么如何判断W的好坏呢. 我们定义一个loss function如下所示:
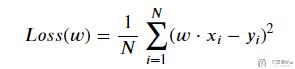
接着我们对其求偏导, 求出w的导数.
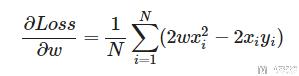
于是, 我们定义求w梯度的式子.
- #返回dJ/dw
- def gradient(x, y, w):
- """计算梯度
- """
- return np.mean(2*w*x*x-2*x*y)
梯度下降
接着我们就可以对参数w进行优化, 有以下的步骤:
- 随机初始化一个w的值;
- 在该w 下进行正向传播, 得到所有x的预测值 y_pre;
- 通过实际的值y和预测值y_pre计算损失;
- 通过损失计算梯度dw;
- 更新w = w-lr*dw, 其中lr为步长(learning rate), 可自定义具体的值;
- 重复步骤2-5, 直到损失降到较小位置;
我们先定义一些变量.
- # 我们先定义一些变量
- def forward(x):
- return w * x
- def loss(y, y_pred):
- return ((y_pred - y)**2).mean()
- w = 0.0 # 初始化系数
- # 定义步长和迭代次数
- learning_rate = 0.001
- n_iters = 100
接着我们使用上面的步骤1-6, 使用梯度下降法, 来求解参数w. 因为我们上面已经是直接对loss进行求导得到了结果, 所在在实际计算的时候, 其实不用forward和计算的loss的.
- for epoch in range(n_iters):
- # 彰显传播
- y_pred = forward(X)
- #计算损失
- # l = loss(Y, y_pred)
- #计算梯度
- dw = gradient(X, Y, w)
- #更新权重 w
- w = w - learning_rate * dw
- if epoch % 20 == 0:
- print(f'epoch {epoch+1}: w = {w:.3f}, loss = {l:.8f}')
- print(f'根据训练模型预测,当 x=7 时,y 的值为: {forward(7):.3f}')
- """
- epoch 1: w = 0.142, loss = 0.06237932
- epoch 21: w = 1.639, loss = 0.06237932
- epoch 41: w = 2.024, loss = 0.06237932
- epoch 61: w = 2.123, loss = 0.06237932
- epoch 81: w = 2.148, loss = 0.06237932
- 根据训练模型预测,当 x=7 时,y 的值为: 15.084
- """
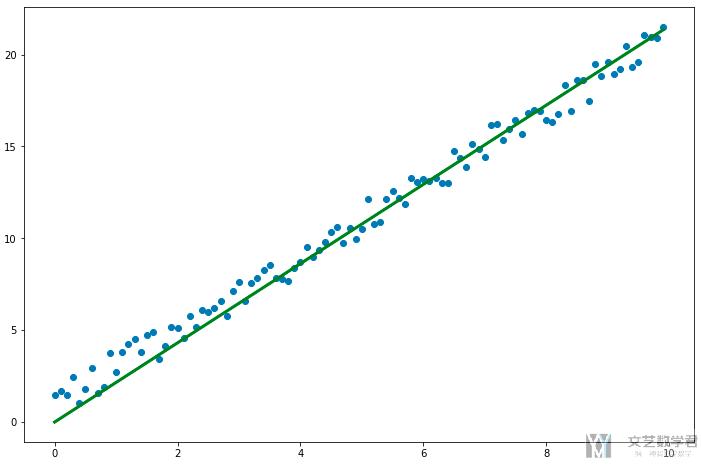
结果可视化
- # 绘制预测曲线
- y_pre = forward(X)
- fig = plt.figure(figsize=(12,8))
- ax = fig.add_subplot(1,1,1)
- ax.scatter(X,Y)
- ax.plot(X, y_pre, 'g-', lw=3)
- fig.show()
最终的结果如下所示:
Pytorch中的梯度下降法
上面我们推导的是一元线性函数的损失函数的梯度公式, 他是比较容易推导的.
但是在实际操作中, 在很多机器学习中, 模型的函数表达式是非常复杂的, 这个时候手动计算梯度就会变得十分复杂. 这个时候就要用到上一篇所讲的.backward(), 使用Pytorch自动求解梯度, 并使用求出的梯度进行梯度下降, 来得到优化的w.
我们还是使用上面的例子来进行说明. 首先我们将变量转换为张量的形式.
- X = np.arange(0,10,0.1, dtype=np.float32)
- Y = 2*X + 2*np.random.random(100)
- X_tensor = torch.from_numpy(X)
- Y_tensor = torch.from_numpy(Y)
- w = torch.tensor(0.0, dtype=torch.float32, requires_grad=True)
- learning_rate = 0.001
- n_iters = 100
接着使用.backward()来进行求梯度, 并进行梯度下降.
- for epoch in range(n_iters):
- y_pred = forward(X_tensor)
- l = loss(Y_tensor, y_pred) # 求误差
- l.backward() # 求梯度
- with torch.no_grad():
- w.data = w.data - learning_rate * w.grad
- # 清空梯度
- w.grad.zero_()
- if epoch % 20 == 0:
- print(f'epoch {epoch+1}: w = {w.item():.3f}, loss = {l.item():.3f}')
- print(f'根据训练模型预测, 当x=5时, y的值为: {forward(5):.3f}')
- """
- epoch 1: w = 0.140, loss = 149.477
- epoch 21: w = 1.618, loss = 10.344
- epoch 41: w = 1.999, loss = 1.151
- epoch 61: w = 2.096, loss = 0.544
- epoch 81: w = 2.121, loss = 0.504
- 根据训练模型预测, 当x=5时, y的值为: 10.638
- """
- 微信公众号
- 关注微信公众号
-

- QQ群
- 我们的QQ群号
-













评论