强化学习解决背包问题

王 茂南
王 茂南
王 茂南
3083
文章
75
评论
2020年8月6日07:19:571 1 5870字阅读19分34秒
摘要这一篇介绍使用强化学习来解决背包问题. 也是作为一个引子,来看一下如何使用强化学习, 来解决这种优化问题.

简介

自己最近在面试关于强化学习相关岗位的时候, 被问到了如何使用强化学习来解决优化问题, 例如背包问题. 其实之前在看强化学习相关内容的时候, 是从来没有想到这些问题的. 那么正好被问到这个问题, 这一篇文章就主要说一下如何使用强化学习来解决背包问题.

关于详细的代码, 可以查看Github链接: 强化学习解决背包问题.ipynb

参考链接(代码部分参考自这个链接, 主要增加了一些解释): 强化学习解决背包问题

 

用强化学习解决背包问题

背包问题简介

现在有N个物品, 分别是n1, n2, ...; 他们的重量分别是w1, w2, w3, ...; 每个物品的价值是v1, v2, v3, ...; 现在有一个能承受重量为C的背包. (注意, 每一个物品都只有一个)

问应该如何放入物品, 使得装入包的物品的价值是最大的.

 

使用强化学习的想法

  • state: 包里目前有的物体情况, 例如有物品1和物品2. 最后会保存为'[1,2]', 就表示包里有1号和2号物品.
  • action: 有N种物品, 就有N中action. 把物品I放入包中, 就是执行动作I.
  • reward: 每放进一个物体, 如果没有超重, reward是物品的value. 如果超重了, reward就是-10, 并且回合结束.

但是还有一个问题是我们需要考虑的, 一个物品被选中后不能选择第二次. 要做到这个要在两个地方进行修改:

  • 我们的想法就是从Q-table来入手. 当有新的状态添加到Q-table中的时候(比如现在状态是[1,3]), 我们就将action 1和action 3的位置设置为NaN, 这样在选max的时候, 就不会选到这些action. 这个在下面函数check_state中有进行实现.
  • 同时我们还需要修改ϵ-greedy的函数. 因为里面有从所有动作里面随机挑一个, 所以我们要有一个列表, 这里存的是所有在当前state下, 可以挑选的动作. 这个具体的实现在函数mu_policy中进行实现.

 

具体代码实现

有了上面简单的介绍, 下面我们来具体实现使用强化学习来解决背包问题.

  1. import pandas as pd
  2. import numpy as np
  3. import matplotlib.pyplot as plt
  4. from time import time
  5. import plotting
  6. import itertools

 

初始化背包

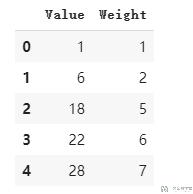
在这个例子里面, 我们的包里面有5种不同的物品, 我们使用dataframe来进行定义. 我们规定重量不能超过11.

  1. item = pd.DataFrame(data=[[1, 1], [6, 2], [18, 5], [22, 6], [28, 7]], columns=['Value', 'Weight'])
  3. actions = list(range(len(item))) # 动作, 每一个物体是一个动作
  4. limit_W = 11 # 背包重量的限制
  5. gamma = 0.9

下面是5种物品详细的value和weight的介绍.

强化学习解决背包问题

 

定义环境

在之前的强化学习的测试里面, 环境都是使用的gym里面的, 这里我们需要自己定义一个环境. 输入的是action和state, 返回reward, 下一个state, 和是否结束(是否超重).

  1. def envReward(action, knapsack):
  2.     """返回下一步的state, reward和done
  3.     """
  4.     limit_W = 11
  5.     knapsack_ = knapsack + [action] # 得到新的背包里的东西, 现在是[2,3], 向里面增加物品[1], 得到新的状态[1,2,3]
  6.     knapsack_.sort()
  8.     knapsack_W = np.sum([item['Weight'][i] for i in knapsack_]) # 计算当前包内物品的总和
  9.     if knapsack_W > limit_W:
  10.         r = -10
  11.         done = True
  12.     else:
  13.         r = item['Value'][action]
  14.         done = False
  15.     return r, knapsack_, done

 

策略的定义

其实在Q-Learning中, 我们只需要使用到一个epsilon-greedy的策略来进行环境的探索(在代码实现的时候).

但是因为Q-Learing是off-policy的方法, 实际上是用到两个策略的. 一个策略用来探索, 另外一个用来实际执行. 所以我们在这里定义的时候, 也是定义两个策略.

  • μ, 定义ϵ-greedy的策略;
  • π, 定义greedy的策略;

下面的ϵ-greedy

  1. def mu_policy(Q, epsilon, nA, observation, actions):
  2.     """
  3.     这是一个epsilon-greedy的策略, 返回每一个动作执行的概率, nA为动作的个数
  4.     其中: 
  5.     - Q是q table, 为dataframe的格式;
  6.     - nA是所有动作的个数
  7.     """
  8.     actionsList = list(set(actions).difference(set(observation))) # 可以挑选的动作
  9.     # 看到这个state之后, 采取不同action获得的累计奖励
  10.     action_values = Q.loc[str(observation), :]
  11.     # 使用获得奖励最大的那个动作
  12.     greedy_action = action_values.idxmax()
  13.     # 是的每个动作都有出现的可能性
  14.     probabilities = np.zeros(nA)
  15.     for i in actionsList:
  16.         probabilities[i] = 1/len(actionsList) * epsilon
  17.     probabilities[greedy_action] = probabilities[greedy_action] + (1 - epsilon)
  18.     return probabilities

接着定义greedy的策略, 这个在训练的时候是不会用到的, 只有在实际使用的时候会用到. 实际执行步骤的时候, value based的方法是完全确定的.

  1. def pi_policy(Q, observation):
  2.     """
  3.     这是greedy policy, 每次选择最优的动作.
  4.     其中: 
  5.     - Q是q table, 为dataframe的格式;
  6.     """
  7.     action_values = Q.loc[str(observation), :]
  8.     best_action = action_values.idxmax() # 选择最优的动作
  9.     return np.eye(len(action_values))[best_action] # 返回的是两个动作出现的概率

 

Q-table的检查

因为这里我们使用的是dataframe来存储的Q-table, 所以一旦有一个新的state出现(比如一开始next state就会是未知的state), 此时我们需要更新Q Table. 我们就在这里定义一个函数来实现这个功能. 同时他还需要确保出现的state不能再次被选择, 也就是一个物品不能选两次.

  1. def check_state(Q, knapsack, actions):
  2.     """检查状态knapsack是否在q-table中, 没有则进行添加
  3.     """
  4.     if str(knapsack) not in Q.index: # knapsack表示状态, 例如现在包里有[1,2]
  5.         # append new state to q table
  6.         q_table_new = pd.Series([np.NAN]*len(actions), index=Q.columns, name=str(knapsack))
  7.         # 下面是将能使用的状态设置为0, 不能使用的设置为NaN (这个很重要)
  8.         for i in list(set(actions).difference(set(knapsack))):
  9.             q_table_new[i] = 0
  10.         return Q.append(q_table_new)
  11.     else:
  12.         return Q

 

开始更新Q-Table

有了上面的一切准备工作之后, 我们就可开始进行模拟, 并更新Q-Table了, 整体的代码如下, 所有地方我都写了注释了.

  1. def qLearning(actions, num_episodes, discount_factor=1.0, alpha=0.7, epsilon=0.2):
  2.     # 环境中所有动作的数量
  3.     nA = len(actions)
  5.     # 初始化Q表
  6.     Q = pd.DataFrame(columns=actions)
  8.     # 记录reward和总长度的变化
  9.     stats = plotting.EpisodeStats(
  10.         episode_lengths=np.zeros(num_episodes+1),
  11.         episode_rewards=np.zeros(num_episodes+1))
  14.     for i_episode in range(1, num_episodes + 1):
  15.         # 开始一轮游戏
  16.         knapsack = [] # 开始的时候背包是空的
  17.         Q = check_state(Q, knapsack, actions)
  18.         action = np.random.choice(nA, p=mu_policy(Q, epsilon, nA, knapsack, actions)) # 从实际执行的policy, 选择action
  19.         for t in itertools.count():
  20.             reward, next_knapsack, done = envReward(action, knapsack) # 执行action, 返回reward和下一步的状态
  21.             Q = check_state(Q, next_knapsack, actions)
  23.             next_action = np.random.choice(nA, p=mu_policy(Q, epsilon, nA, next_knapsack, actions)) # 选择下一步的动作
  24.             # 更新Q
  25.             Q.loc[str(knapsack), action] = Q.loc[str(knapsack), action] + alpha*(reward + discount_factor*Q.loc[str(next_knapsack), :].max() - Q.loc[str(knapsack), action])
  27.             # 计算统计数据(带有探索的策略)
  28.             stats.episode_rewards[i_episode] += reward # 计算累计奖励
  29.             stats.episode_lengths[i_episode] = t # 查看每一轮的时间
  31.             if done:
  32.                 break
  34.             if t > 10:
  35.                 break
  37.             knapsack = next_knapsack
  38.             action = next_action
  40.         if i_episode % 50 == 0:
  41.             # 打印
  42.             print("\rEpisode {}/{}. | ".format(i_episode, num_episodes), end="")
  44.     return Q, stats

最后我们模拟1000次, 看一下最终的结果:

  1. Q, stats = qLearning(actions, num_episodes=1000, discount_factor=0.9, alpha=0.3, epsilon=0.1)

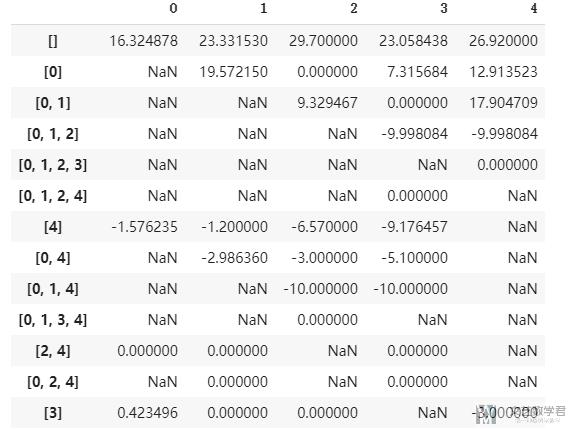
最后部分的Q-Table如下图所示, 完整的Q-Table见Github仓库, 里面还包括reward的变化图: 强化学习解决背包问题.ipynb

强化学习解决背包问题

 

结果测试

在有了上面的Q-Table之后, 我们看一下实际运行结果是什么样子的.

  1. # 查看最终结果
  2. actionsList = []
  3. knapsack = [] # 开始的时候背包是空的
  4. nA = len(actions)
  6. action = np.random.choice(nA, p=pi_policy(Q, knapsack)) # 从实际执行的policy, 选择action
  8. for t in itertools.count():
  9.     actionsList.append(action)
  10.     reward, next_knapsack, done = envReward(action, knapsack) # 执行action, 返回reward和下一步的状态
  11.     next_action = np.random.choice(nA, p=pi_policy(Q, next_knapsack)) # 选择下一步的动作
  12.     if done:
  13.         actionsList.pop()
  14.         break
  15.     else:
  16.         action = next_action
  17.         knapsack = next_knapsack

最后选择结果是2和3, 此时重量刚好是11, 且价值达到最大, 是40. 以上为使用强化学习来解决背包问题的全部内容.

  • 微信公众号
  • 关注微信公众号
  • weinxin
  • QQ群
  • 我们的QQ群号
  • weinxin
王 茂南
  • 本文由 发表于 2020年8月6日07:19:57
  • 转载请务必保留本文链接：https://mathpretty.com/12560.html
匿名

发表评论

匿名网友 填写信息

:?: :razz: :sad: :evil: :!: :smile: :oops: :grin: :eek: :shock: :???: :cool: :lol: :mad: :twisted: :roll: :wink: :idea: :arrow: :neutral: :cry: :mrgreen:

评论：1   其中：访客  1   博主  0
    • guava
      guava
      2021年5月5日 下午4:28 1F
      回复

      您好，想請問若想解決的是多目標背包問題的話，例如有N個物品要放入P個背包，這個方法是否可行或是能用何種方法解決，謝謝。