Pytorch实现Actor Critic Baseline (A2C, Cliff Walking PlayGround)

王 茂南
王 茂南
王 茂南
3084
文章
75
评论
2020年8月21日07:21:21
评论1 6637字阅读22分7秒
摘要这一篇简单介绍使用Pytorch在环境Cliff Walking PlayGround上实现Actor-Critic Baseline (A2C). 因为目前很少有使用Cliff Walking作为A2C的例子, 这里就做一个简单的说明. 最后会把原始的notebook文件上传Github.

简介

这一篇介绍在Policy Gradient中的Actor Critic Baseline, 也就是常说的A2C. 这一篇的实验环境还是使用Cliff Walking PlayGround, 使用Google Colab完成实验.

这一篇会简单介绍一下Policy Gradient with Baseline的算法过程 (关于具体的推导, 放在之后来讲), 本文会使用Pytorch实现简单的A2C.

参考资料

 

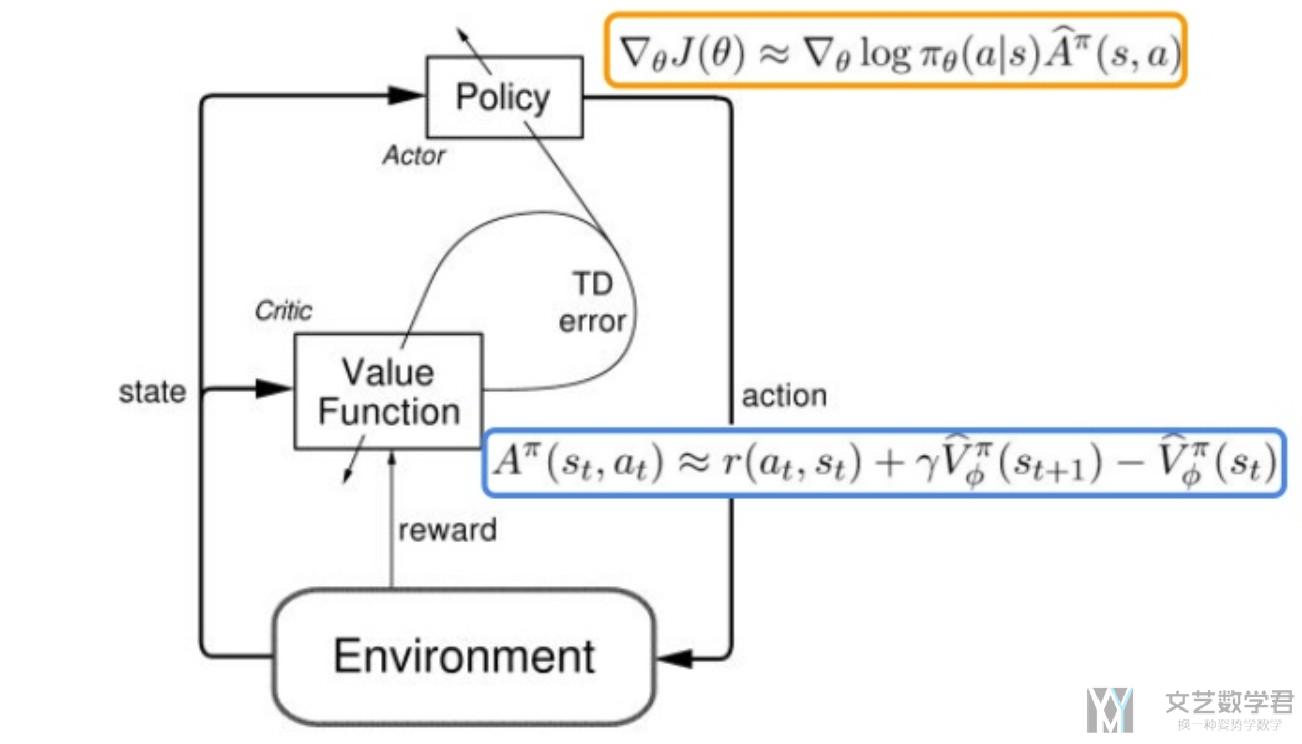
Actor Critic Baseline的介绍

Actor Critic是Policy Gradient算法. 他的想法就是希望可以找到一个函数, 来近似Policy, 给这个函数state, 返回的是每一个动作的action. 一般我们会称这个policy为Pi.

为了更新这个策略, 我们需要定义目标函数, 目标函数是希望累计reward尽可能大. 经过化简有以下的形式, 其中Pi(s,a)是用来根据state, 给出action的概率. 除此之外, 我们还需要估计state-action value, 也就是Q值.

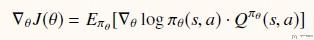
Pytorch实现Actor Critic Baseline (A2C, Cliff Walking PlayGround)

为了减少方差, 我们定义了一个advantage function, 为A = Q - V, 目的是保持上面的期望不变, 方差减少. 如下所示, 但是这样有一个问题, 就是我们需要近似三个函数, 分别是Pi, Q, V.

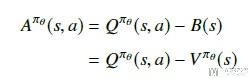
Pytorch实现Actor Critic Baseline (A2C, Cliff Walking PlayGround)

但是, 我们可以证明V的TD误差是上面A的无偏估计. 所以最终的梯度公式可以化简为如下的形式.

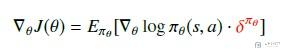
Pytorch实现Actor Critic Baseline (A2C, Cliff Walking PlayGround)

其中:

Pytorch实现Actor Critic Baseline (A2C, Cliff Walking PlayGround)

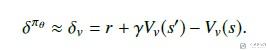
其中Pi和V我们都可以使用神经网络进行代替, 梯度也是可以进行求的. 于是上面的式子就是可以求得. 下面看一下完整的算法流程.

 

Actor Critic Baseline算法流程

我们把上面的方法稍作归纳, 可以写成下面的形式.

Pytorch实现Actor Critic Baseline (A2C, Cliff Walking PlayGround)

其中:

  • 为了更新critic function, 我们设置loss function为(V-Gt)^2, 求导后与上面的式子相同.
  • 为了更新actor function, 我们设置loss function为-log_prob * (Gt - V), 这里我们增加负号, 于是可以使用梯度下降来进行参数更新.

下面是我从Actor critic algorithm看到的, 很好的介绍了算法的流程, 就放在这里做一个总体的参考.

Pytorch实现Actor Critic Baseline (A2C, Cliff Walking PlayGround)

 

Pytorch实现Actor Critic Baseline (A2C)

这里我们只给出关键部分的代码, 完成的notebook可以查看github仓库,

初始化环境

我们这里还是使用Cliff Walking Playground, 先初始化环境.

  1. env = CliffWalkingEnv()

接着我们定义一个函数, 来获取当前的state. 因为在Cliff Walking Playground只会返回当前的state, 也就是一个数字, 我们在这里将其转换为one-hot的向量.

  1. def get_screen(state):
  2.     """这里我们就用state来作为例子, 不直接使用截图了, 将编号转换为one-hot向量, 共48维
  3.     """
  4.     y_state = torch.Tensor([[state]]).long()
  5.     y_onehot = torch.FloatTensor(1, 48) # 产生位置
  6.     # In your for loop
  7.     y_onehot.zero_() # 全部使用0进行填充
  8.     y_onehot.scatter_(1, y_state, 1) # 返回one-hot
  9.     return y_onehot

比如说, 如果环境返回的是state=1, 那么该函数就可以生成如下的向量.

  1. get_screen(1)
  2. """
  3. tensor([[0., 1., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
  4.          0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
  5.          0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.]])
  6. """

 

定义Actor Critic的模型

首先我们简单来看一下Actor和Critic这两个模型的输入和输出.

  • Actor模型的输入是state, 输出是每一个action的概率.
  • Critic模型的输入是state, 输入是这个state对应的value.

所以这两个模型的输入部分都是对state的处理, 所以我们可以将这两个网络的前几层进行共享. 下面我们定义模型, 定义在一个class里面, 输出部分由两个部分组成.

  1. class ActorCriticModel(nn.Module):
  2.     def __init__(self):
  3.         super(ActorCriticModel, self).__init__()
  4.         self.fc1 = nn.Linear(48, 24)
  5.         self.fc2 = nn.Linear(24, 12)
  6.         self.action = nn.Linear(12, 4)
  7.         self.value = nn.Linear(12, 1)
  8.     def forward(self, x):
  9.         x = F.relu(self.fc1(x))
  10.         x = F.relu(self.fc2(x))
  11.         action_probs = F.softmax(self.action(x), dim=-1)
  12.         state_values = self.value(x)
  13.         return action_probs, state_values

于是, Actor模型和Critic模型的结构分别如下:

  • Actor模型的结构是, 48->24->12->4;
  • Critic模型的结构是, 48->24->12->1;

前面两层的参数是共享的. 这个网络的输出有两个, 一个是actor模型的返回, 每个action的概率, 另一个是这个state的value值. 我们简单看一下这个网络的返回.

  1. ac = ActorCriticModel()
  2. action_probs, state_values = ac(get_screen(1).squeeze(0))
  3. print(action_probs)
  4. print(state_values)
  5. """
  6. tensor([0.2140, 0.3271, 0.2130, 0.2459], grad_fn=<SoftmaxBackward>)
  7. tensor([-0.3331], grad_fn=<AddBackward0>)
  8. """

 

模型的训练

在这里我们使用MC的方式来进行训练. 我们会完成一个完整的episode, 这个时候可以获得如下的一组数据:

  • 当前state的累计收益(Gt, 这个是实际计算的);
  • 对当前state收益的估计(V值);
  • 当前state采取一个action的概率的log值, 即对应下面代码中的log_probs;

接着, 我们可以计算actor loss和critic loss. 这两个loss的计算分别如下:

  • critic loss = (V-Gt)^2, 也就是希望我们对状态state的价值估计与其实际价值相似.
  • actor loss = -log_prob * (Gt - V), 我们称作Gt-V为advantage function.

于是, 将上面的想法合起来, 就组成了下面的代码.

  1. def trainIters(env, ActorCriticModel, num_episodes, gamma = 0.9):
  2.     optimizer = torch.optim.Adam(ActorCriticModel.parameters(), 0.03) # 注意学习率的大小
  3.     scheduler = torch.optim.lr_scheduler.StepLR(optimizer, step_size=10, gamma=0.9)
  5.     # 记录reward和总长度的变化
  6.     stats = plotting.EpisodeStats(
  7.         episode_lengths=np.zeros(num_episodes+1),
  8.         episode_rewards=np.zeros(num_episodes+1))
  10.     for i_episode in range(1, num_episodes+1):
  11.         # 开始一轮游戏
  12.         state = env.reset() # 环境重置
  13.         state = get_screen(state) # 将state转换为one-hot的tensor, 用作网络的输入.
  15.         log_probs = []
  16.         rewards = []
  17.         state_values = []
  19.         for t in itertools.count():
  20.             action_probs, state_value = ActorCriticModel(state.squeeze(0)) # 返回当前state下不同action的概率
  22.             action = torch.multinomial(action_probs, 1).item() # 选取一个action
  23.             log_prob = torch.log(action_probs[action])
  24.             next_state, reward, done, _ = env.step(action) # 获得下一个状态
  26.             # 计算统计数据
  27.             stats.episode_rewards[i_episode] += reward # 计算累计奖励
  28.             stats.episode_lengths[i_episode] = t # 查看每一轮的时间
  30.             # 将值转换为tensor
  31.             reward = torch.tensor([reward], device=device)
  32.             next_state_tensor = get_screen(next_state)
  34.             # 将信息存入List
  35.             log_probs.append(log_prob.view(-1))
  36.             rewards.append(reward)
  37.             state_values.append(state_value)
  39.             # 状态更新
  40.             state = next_state_tensor
  42.             if done: # 当一轮结束之后, 开始更新
  43.                 returns = []
  45.                 Gt = 0
  46.                 pw = 0
  48.                 # print(rewards)
  49.                 for reward in rewards[::-1]:
  50.                     Gt = Gt + (gamma ** pw) * reward # 写成Gt += (gamma ** pw) * reward, 最后returns里东西都是一样的
  51.                     # print(Gt)
  52.                     pw += 1
  53.                     returns.append(Gt)
  55.                 returns = returns[::-1]
  57.                 returns = torch.cat(returns)
  58.                 returns = (returns - returns.mean()) / (returns.std() + 1e-9)
  59.                 # print(returns)
  60.                 log_probs = torch.cat(log_probs)
  61.                 state_values = torch.cat(state_values)
  63.                 # print(returns)
  64.                 # print(log_probs)
  65.                 # print(state_values)
  67.                 advantage = returns.detach() - state_values
  69.                 critic_loss = F.smooth_l1_loss(state_values, returns.detach())
  70.                 actor_loss = (-log_probs * advantage.detach()).mean()
  71.                 loss = critic_loss + actor_loss
  73.                 # 更新critic
  74.                 optimizer.zero_grad()
  75.                 loss.backward()
  76.                 optimizer.step()
  78.                 print('Episode: {}, total steps: {}'.format(i_episode, t))
  80.                 if t>20:
  81.                     scheduler.step()
  83.                 break
  85.     return stats

上面代码可以说是由两个部分组成的:

  • 对于每一个episode, 我们都进行模型, 使用actor生成动作, 并使用critic得到对state的评价, 将其分别存入数组中.
  • 当一个episode结束后, 我们根据返回的reward, 分别计算每一个state的累计reward. 也就是上面for reward in reward[::-1]部分的代码. 接着就是计算两个的loss, 并进行反向传播, 更新网络参数.

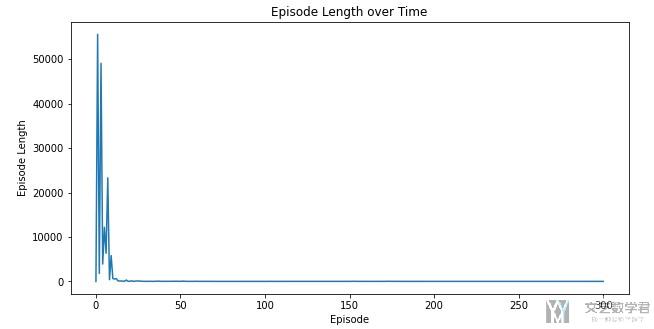
大概可以在20个episode之后模型收敛.

Pytorch实现Actor Critic Baseline (A2C, Cliff Walking PlayGround)

一些注意点

上面的代码中, 有几个小的tricks, 在这里说明一下. 第一个是一定要对returns进行归一化处理. 也就是下面这句语句.

  1. returns = (returns - returns.mean()) / (returns.std() + 1e-9)

如果去掉之后, 好像是不能收敛的.

第二个是关于计算Gt的时候, 如果已经是tensor的格式, 不能使用简写符号, 这样会使得内存共享, 导致最后returns数组里的结果是完全一些的. 也就是不能写成下面的形式>

  1. Gt += (gamma ** pw) * reward,

需要写成下面的形式, 这一这里说的情况是reward已经是tensor的格式了.

  1. Gt = Gt + (gamma ** pw) * reward

 

  • 微信公众号
  • 关注微信公众号
  • weinxin
  • QQ群
  • 我们的QQ群号
  • weinxin
王 茂南
  • 本文由 发表于 2020年8月21日07:21:21
  • 转载请务必保留本文链接：https://mathpretty.com/12665.html
匿名

发表评论

匿名网友 填写信息

:?: :razz: :sad: :evil: :!: :smile: :oops: :grin: :eek: :shock: :???: :cool: :lol: :mad: :twisted: :roll: :wink: :idea: :arrow: :neutral: :cry: :mrgreen: