参数估计之点估计

点估计：

设x1,x2,...,xn是来自总体的一个样本，用于估计未知参数θ的统计量称为θ的估计量，或称为θ的点估计，简称估计。

下面介绍几种常用的点估计方法并给出相应的mathematica程序举例实现。

1.矩估计

• 概念：矩估计法，也称“矩法估计”，就是利用样本矩来估计总体中相应的参数。首先推导涉及感兴趣的参数的总体矩（即所考虑的随机变量的幂的期望值）的方程，然后取出一个样本并从这个样本估计总体矩，接着使用样本矩取代（未知的）总体矩，解出感兴趣的参数，从而得到那些参数的估计。

• 说明：矩估计可能不是唯一的，并且在求矩估计时，尽量采用 低阶矩 给出未知参数的估计。

• mathematica实现矩估计：

(*举例贝塔分布*)

dist1 = RandomVariate[BetaDistribution[3, 3],1000];
(*产生符合参数为3，3的贝塔分布的100个数据*)
EstimatedDistribution[dist1, BetaDistribution[\[Alpha], \[Beta]], ParameterEstimator-> "MethodOfMoments"]
(*矩估计函数，依次写入数据集，分布形式，参数估计计算方法*)
>>BetaDistribution[3.15154, 3.11812]

(*举例伯努利分布*)
dist2 = RandomVariate[BinomialDistribution[100, 0.4], 1000];
(*产生符合二项分布b（100，0.4）的100个数据*)
EstimatedDistribution[dist2, BinomialDistribution[n, p],ParameterEstimator -> "MethodOfMoments"]
(*得到参数估计的结果*)
>>BinomialDistribution[98.0843, 0.406395]

• 用mathematica检验估计效率

(*方法一：画图检验*)
data1 = EstimatedDistribution[dist1, BetaDistribution[\[Alpha], \[Beta]], ParameterEstimator -> "MethodOfMoments"];
(*把上述估计贝塔分布的结果存入data1*)
Show[Histogram[dist1, Automatic, "ProbabilityDensity"], Plot[PDF[data1, x], {x, 0, 50}]]
(*将真实分布的直方图和估计分布的pdf画在同一张图上作比较，由于使用了pdf所以只能比较连续分布的估计效率*)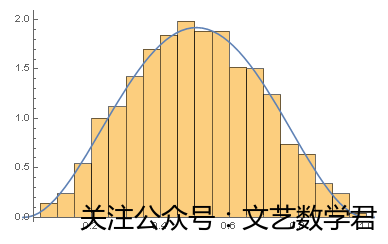

结果拟合的在一定水平上可以认为较好。

(*方法二：使用分布拟合检验函数*)
DistributionFitTest[dist1, data1, {"TestDataTable", All}]
(*参数依次为原始数据，得到的估计分布的数据，表格显示内容*)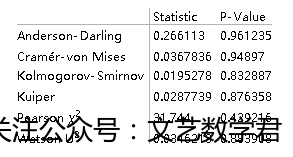

该假设检验的原假设为：估计得出的数据是和真正数据来自同一分布的。由表中数据可知，p值均较大，所以可以在一定的置信水平上认为两组数据来自同一分布，即矩估计结果较为准确。

2.最大似然估计（MLE）

• 概念：关于最大似然有个有趣的比喻：假如有两个一摸一样的箱子，第一个箱子有99个白球1个黑球，第二个箱子有1个白球，99个黑球，现在从两个箱子中随机挑选一个并从中随机抽取一球，得到的是白球，那么这个箱子很可能是第一个箱子，这就类似于最大似然的意思。在对总体中的未知参数θ进行估计时，将样本的联合概率函数看成是θ的函数，此即称为样本的似然函数，如果有一个统计量使得似然函数达到最大值，那么这和统计量就叫做最大似然估计，记为MLE。

• 说明：最大似然估计通常都有渐进正态性。

• mathematica实现最大似然估计：

有多种实现最大似然估计的方法，这里采用直观的图像方法

(*对单参数的最大似然估计：举例上述伯努利分布*)
dist2 = RandomVariate[BinomialDistribution[100, 0.4], 1000];
Show[Plot[LogLikelihood[BinomialDistribution[100, p], dist2], {p, 0, 1}]]
(*在直角坐标系中画出参数p取值在（0，1）内各点时其似然值的变化曲线*)
(*也可以通过FindMaximun来求出最大值点*)
FindMaximum[
LogLikelihood[BinomialDistribution[100, p], dist2], {p, 0.1}]
>> {-2964.33, {p -> 0.40176}}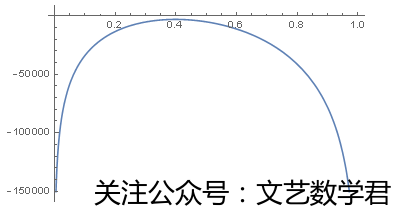

从图中可以看到最大值在p=0.4时取到。

(*对双参数的最大似然估计：举例上述贝塔分布*)
dist1 = RandomVariate[BetaDistribution[3, 3],1000];
ContourPlot[LogLikelihood[BetaDistribution[\[Alpha], \[Beta]], dist1], {\[Alpha],1, 6}, {\[Beta], 2, 6}]
(*对上述贝塔分布进行最大似然估计，使用ContourPlot函数画出似然值等高线图，可以确定似然值最大的参数范围*)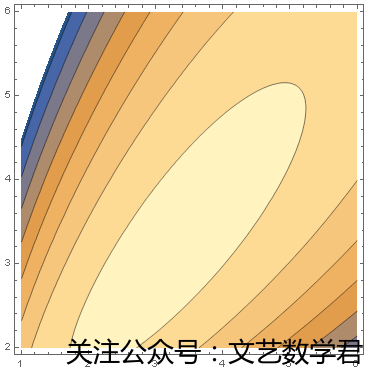

参数（3，3）大约处于等高线最大值的中心位置，在中心附近的值都可以参考采取。

(*类似上面的例子，举例正态分布*)
dist3 = RandomVariate[NormalDistribution[2, 9], 1000];
ContourPlot[LogLikelihood[NormalDistribution[\[Alpha], \[Beta]],dist3], {\[Alpha], 0, 5}, {\[Beta], 7, 11}]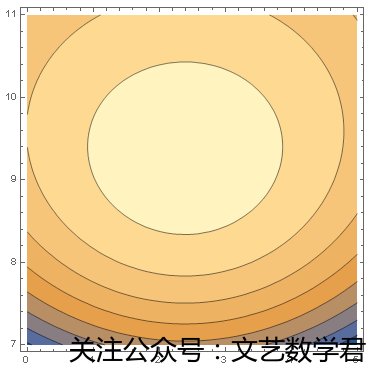

当然我们也可以画出3维的图像来

maxPonit =
FindMaximum[
LogLikelihood[NormalDistribution[\[Alpha], \[Beta]],
dist3], {\[Alpha], \[Beta]}];
Plot3D[LogLikelihood[NormalDistribution[\[Alpha], \[Beta]],
dist3], {\[Alpha], 0, 5}, {\[Beta], 7, 11},
ColorFunction -> Function[{x, y, z}, Hue[.65 (1 - z)]],
PlotLabel ->
Style["parameter estimation : " <> ToString@Last[maxPonit], Bold,
14]]~Show~
Graphics3D[{Black, PointSize[.04],
Point[{\[Alpha], \[Beta], maxPonit[[1]]} /. Last[maxPonit]]}]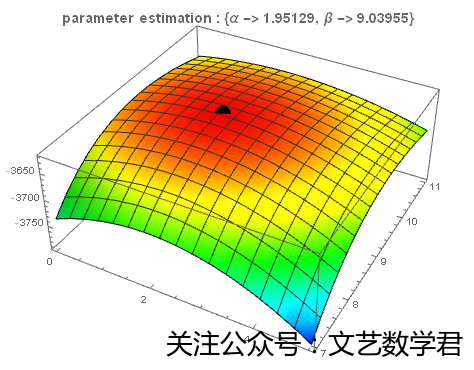

但是像均匀分布这样的分布函数，其似然函数是一个示性函数，无法通过以上的连续画图得到最大值点，但因为均匀分布的两个参数的最大似然估计可以通过计算得到，其值就是样本最大值和最小值，所以简单来用可以直接编写计算。

dist4 = RandomVariate[UniformDistribution[{1, 2}], 1000];
A = Sort[dist4]; (*对样本排序*)
a = A[[1]]
b = A[[1000]]
>>1.00036
>>1.99964

其结果距离真值（1，2）较为接近。