一元,二元泰勒展开-图解高等数学03

一元,二元泰勒展开

• 文章转自：微信号 meetmath
• 由@文艺数学君@王茂南整理修订并发布

泰勒公式是用相对简单的多项式函数去近似复杂的函数(光滑).

一元函数的泰勒展开

如果是一阶的泰勒展开多项式, 可以看到就是在某点的切线, 它的斜率就是在曲线该点的导数, 这个就是"以直代曲"的思想。

当然, 对于曲线的其他部分而言, 只用该点的切线来替代, 还是不够充分, 那就进行更高阶的泰勒展开, 当有了更多的资讯(更高阶导数的信息), 近似这个曲线的程度会越来越好. （在某一点处进行展开，会在那点附件进行逼近，阶数越高，逼近范围可以越大）

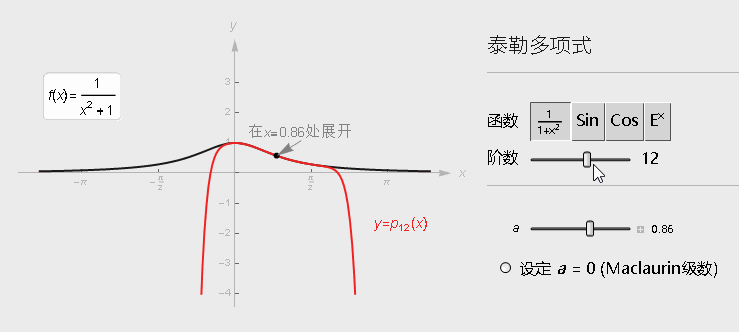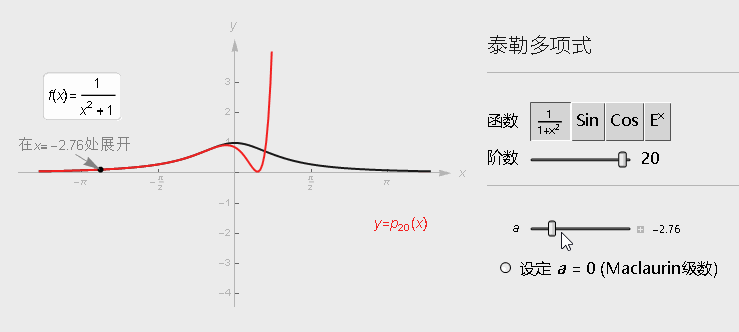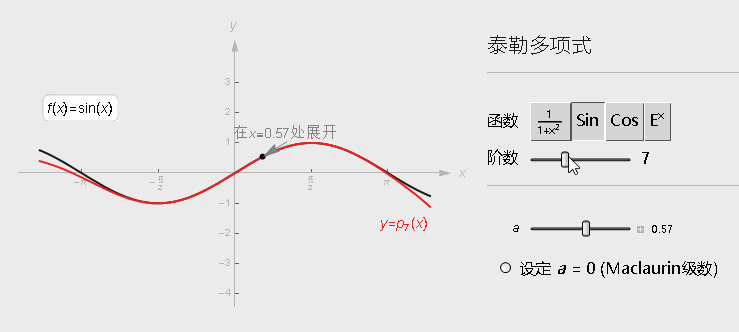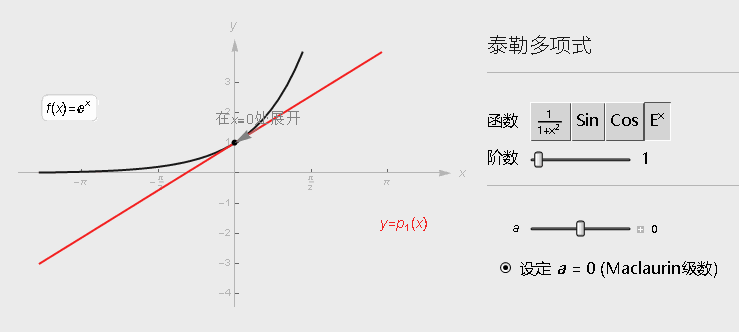
下面是一元函数在x_k处展开的公式：

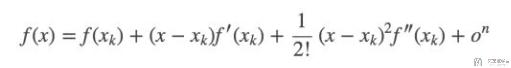
二元函数的泰勒公式展开

相应于一元, 可以进行类比思考, 二元函数的一阶展开多项式就是一个切平面了, 更高阶的时候也会越来越逼近原函数, 从下图可以观察整个变化

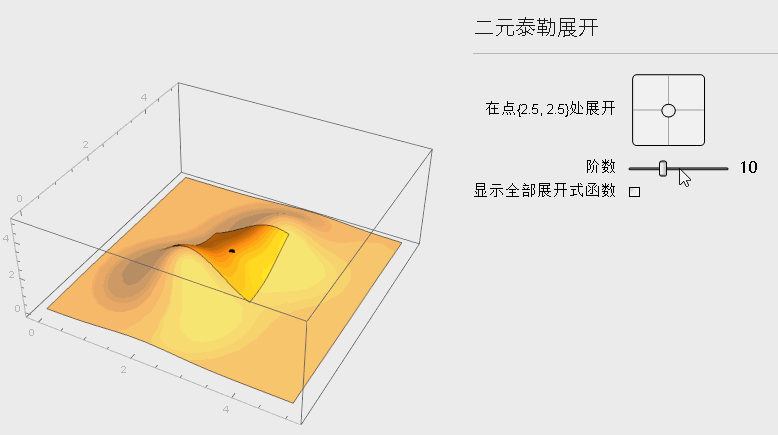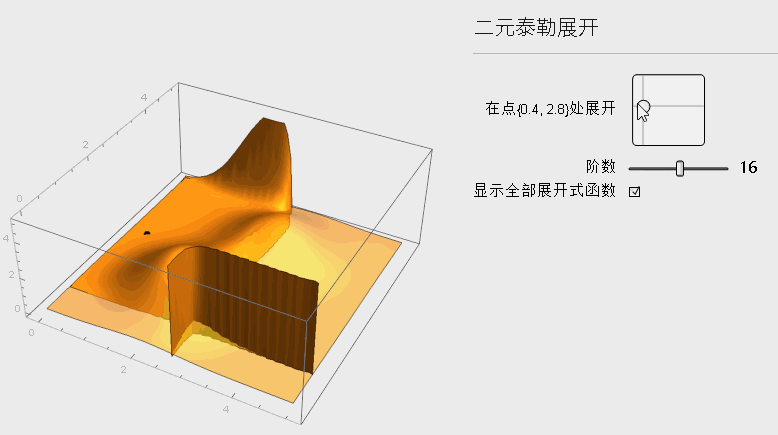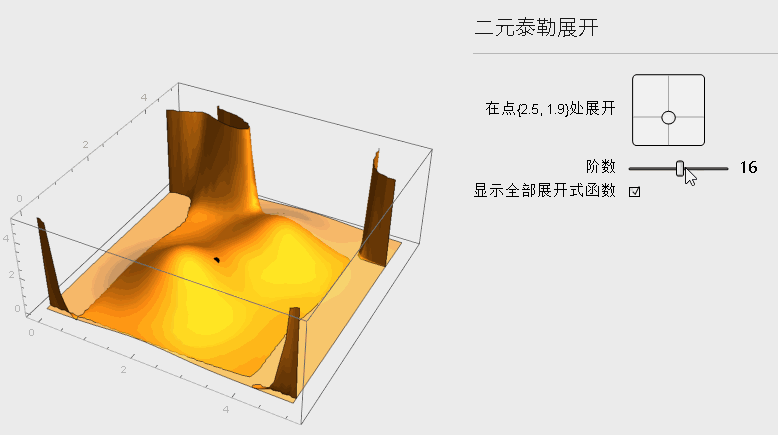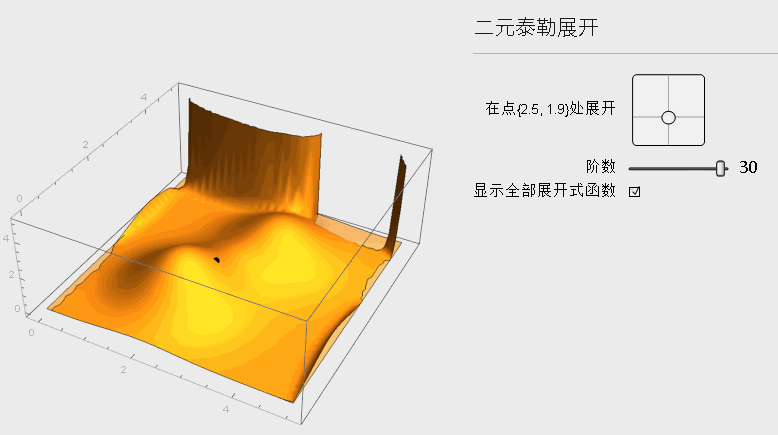
下面是二元函数在x_k处展开的公式：

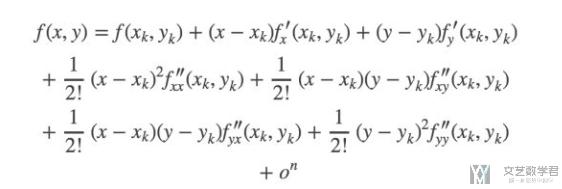
多元函数的泰勒展开

由于多元函数无法绘制图像，我们就直接看一下多元函数泰勒公式最后的表达式：

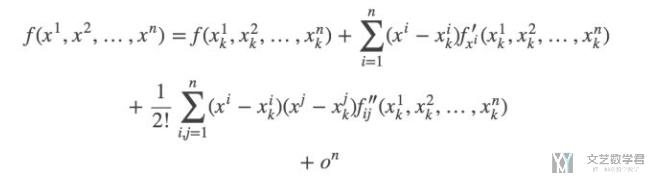
我们一般会写成矩阵的形式，矩阵形式如下所示：

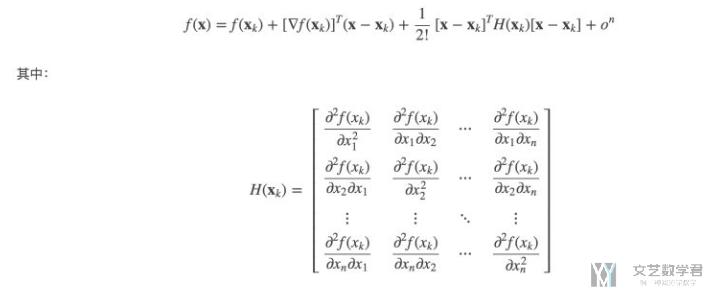
结束语

上面就是利用 Wolfram 语言制作的图解高等数学例子. 好了, 现在让我们在下一篇的中来看一看其他高等数学相关的动图.

感谢关注! Happy Weekend!