三重积分-图解高等数学13

概述

• 文章转自：微信号 meetmath
• 由@文艺数学君@王茂南整理修订并发布

图解高等数学系列, 是以动图的形式将的数学知识点展示出来.

希望该系列能够帮助朋友更加深刻的理解某些较为抽象的概念. 也因为本人水平有限, 疏忽错误在所难免, 所以还请各位老师和朋友不吝赐教, 多提宝贵意见, 帮助我改进这个系列, 先感谢感谢啦!

这一部分会介绍关于三重积分的相关问题, 直观的了解一下三重积分是如何进行计算的.

积分回顾

先来回顾一下, 让我们用物理上的质量为例来理解定积分和二重积分的概念会十分有帮助:

定积分: 长度为[a,b], 且线密度 f(x) 的质线的质量,  其中 dx 是表示一个很小区间的微元.

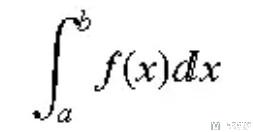
二重积分: 区域为 D, 且面密度为 f(x,y)的平面薄片的质量, 其中 dσ 表示一个很小区域的面积

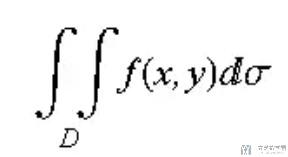
三重积分: 从上面可以看出积分是用来计算某个区域上分布律非均匀的某种量的总和, 那对于三重积分的物理意义, 用类比的思想来考虑, 那就是计算三维物体的质量. 也就是对于空间区域为Ω, 且以 f(x,y,z) 为体密度的立体质量:

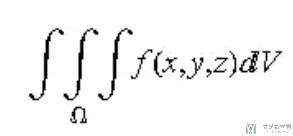
其中 dV 表示一个很小的方块体积, 乘以体密度 f(x,y,z) 就等于在 (x,y,z) 处质量, 取小块直径极限为 0 , 在空间区域 Ω 累加求和, 即可得出该物体质量.

在直角坐标系下的计算公式 - 柱线法

先来看看如下图空间区域为Ω的物体:

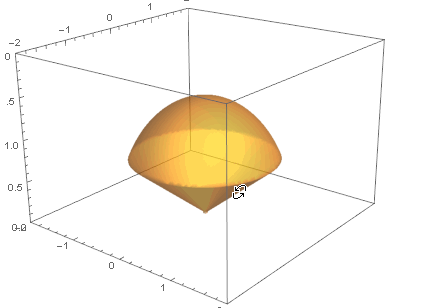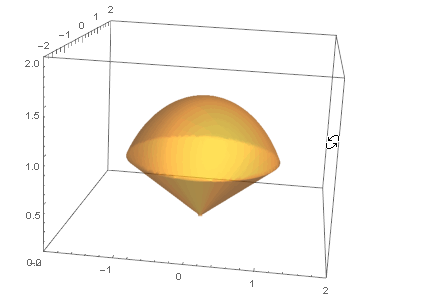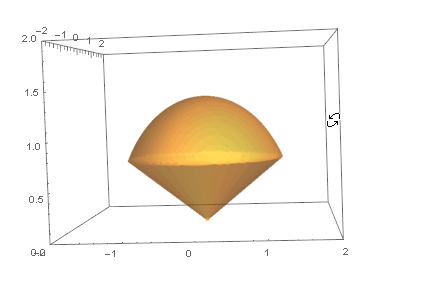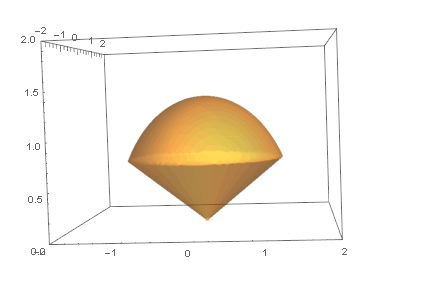
计算该物体的质量的三重积分, 步骤也跟二重一样: 分割 - 求和 - 取极限:

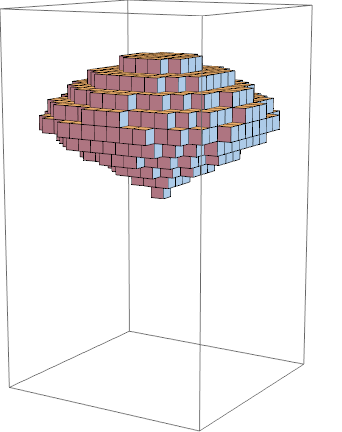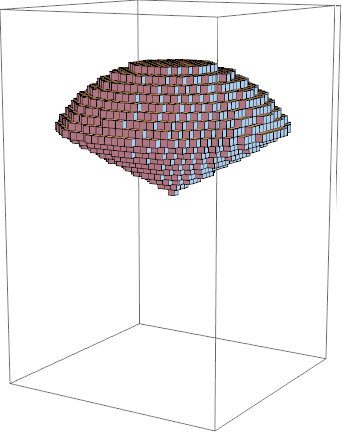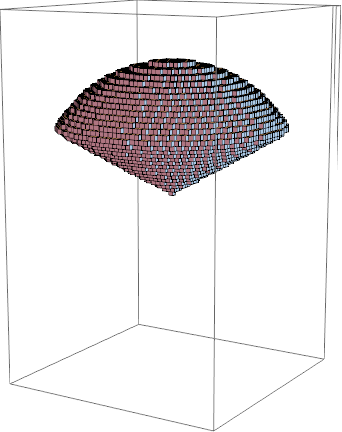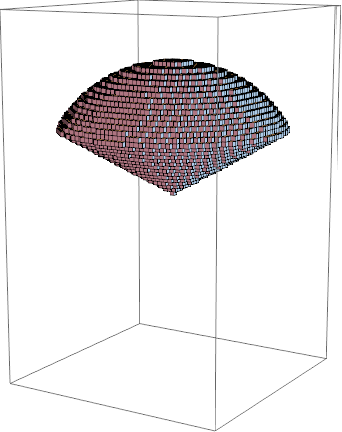
计算质量分布非均匀空间区域为Ω的物体的质量:

• 分割 - 将区域Ω分为n个平行于z轴细长条
• 取近似 - 求每个小长条的质量(体密度*小方块, 然后取极限)

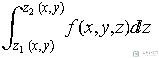
再将这些区域D的小长条质量加总, 而这些就跟二重积分计算方法完全一样. 可以查看下面的动态图片来理解整个过程(为了更好说明问题, 我换用了另一个空间物体)

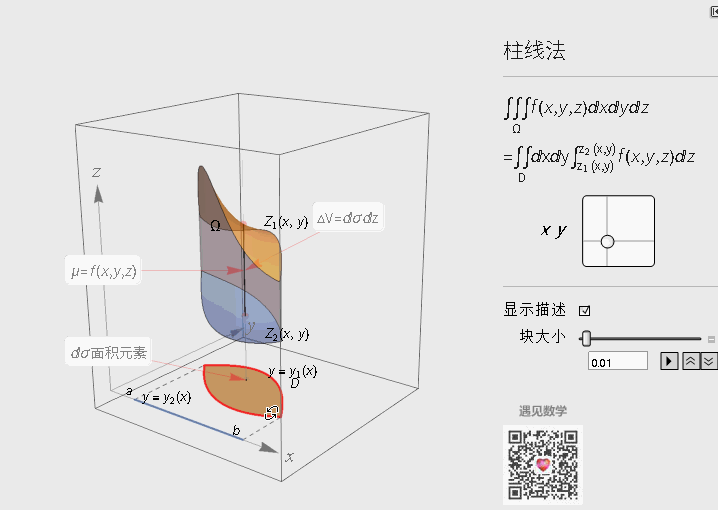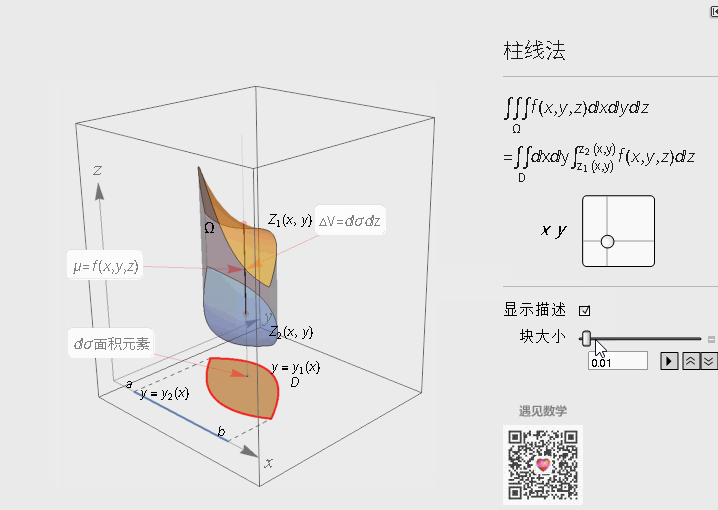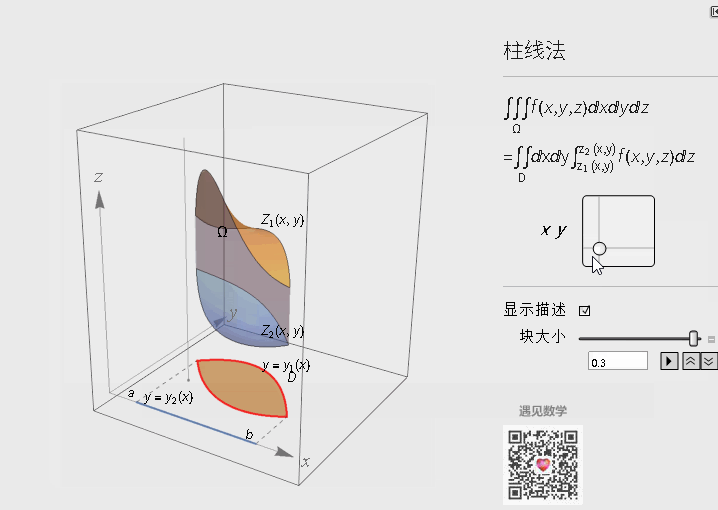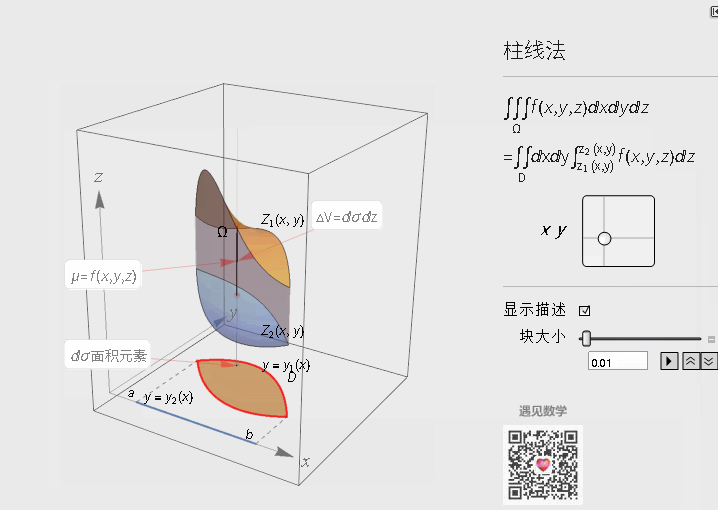
另外截面法来求三重积分, 原理一样, 我在这一个版本中不再编写模型.

结束语

上面就是利用 Wolfram 语言制作的图解高等数学例子. 好了, 现在让我们在下一篇的中来看一看其他高等数学里相关概念动图.

感谢关注! Thanks!