投影及其应用-图解高等数学16

概述

• 文章转自：微信号 meetmath
• 由@文艺数学君@王茂南整理修订并发布

图解高等数学系列, 是以动图的形式将的数学知识点展示出来.

希望该系列能够帮助朋友更加深刻的理解某些较为抽象的概念. 也因为本人水平有限, 疏忽错误在所难免, 所以还请各位老师和朋友不吝赐教, 多提宝贵意见, 帮助我改进这个系列, 先感谢感谢啦!

这一部分会简单介绍一下投影的相关知识. 在介绍第一类曲面积分之前, 有必要先再回顾看下投影的概念以及简单计算椭圆面积应用.

投影的相关知识

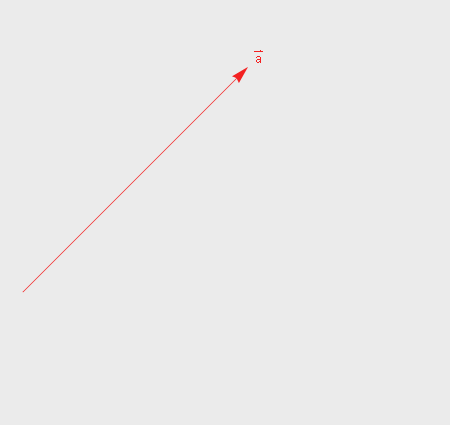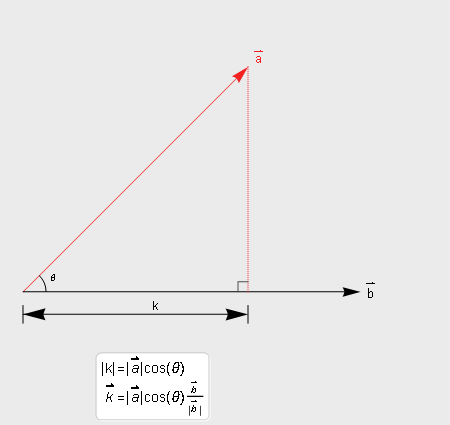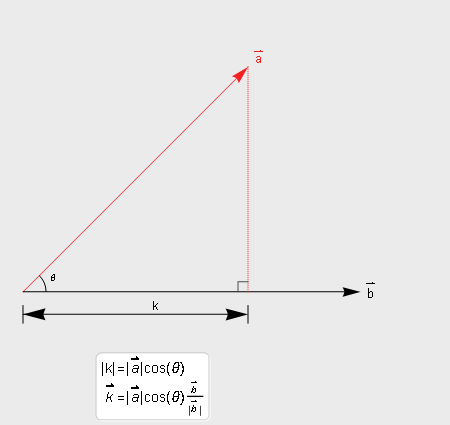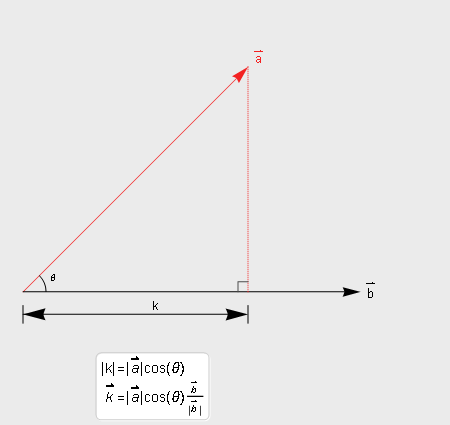
向量a在b方向的投影量

a在b方向的投影量长度k = |a|cosθ, 当然如果要求的是投影向量就还需要乘以b的单位向量.

面的投影

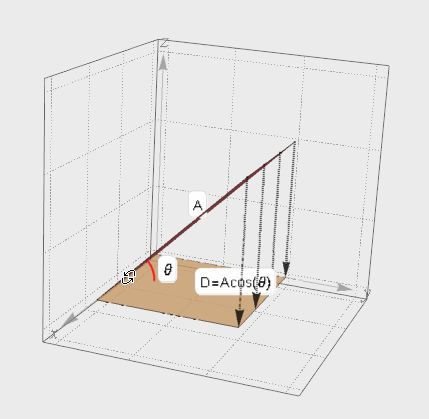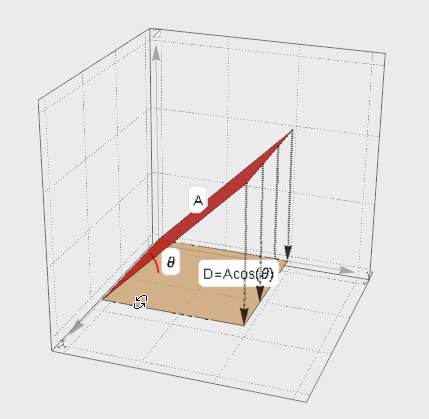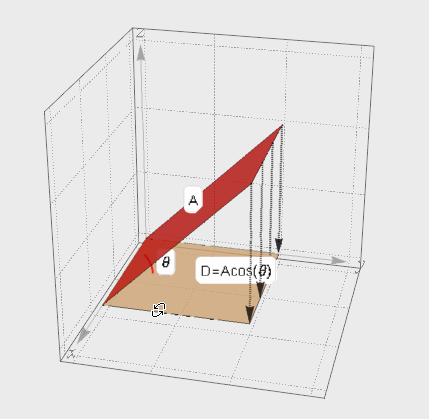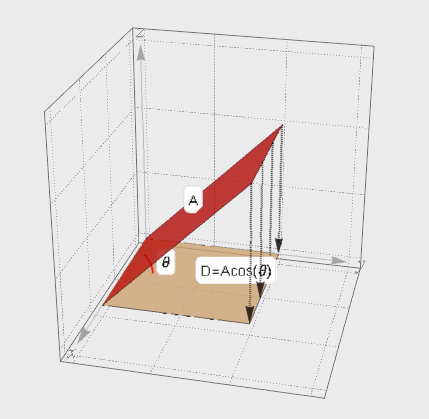
介绍完向量的投影, 再来看面的投影. A在夹角θ方向上的投影面D. 考虑D的面积肯定要比A要小, 但是小多少呢? 其实根据上面向量投影的思想就可以知道投影面积D=A*cos(θ)

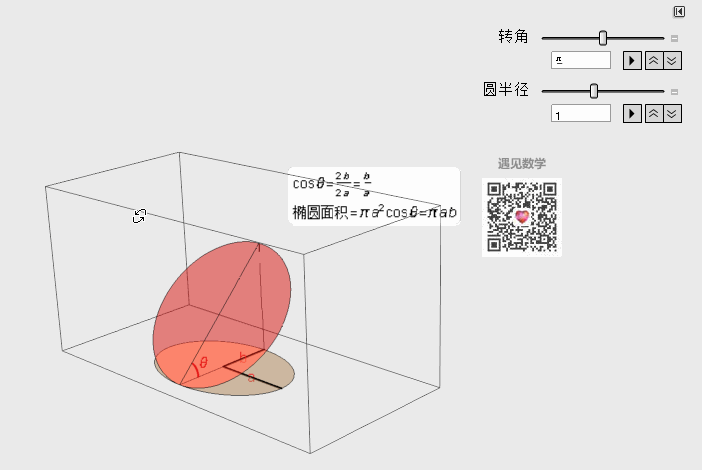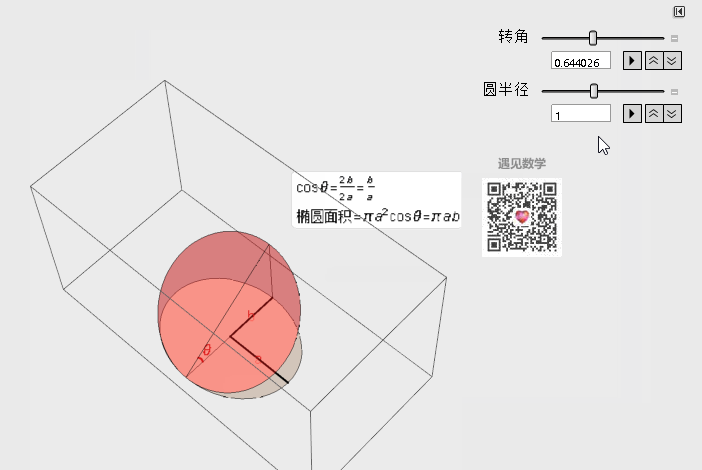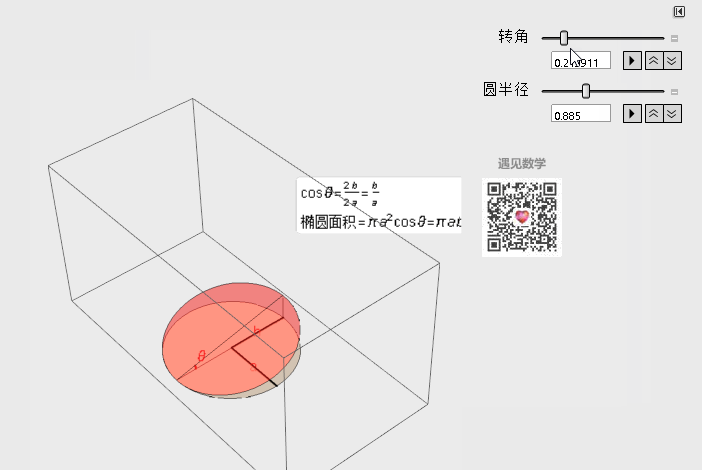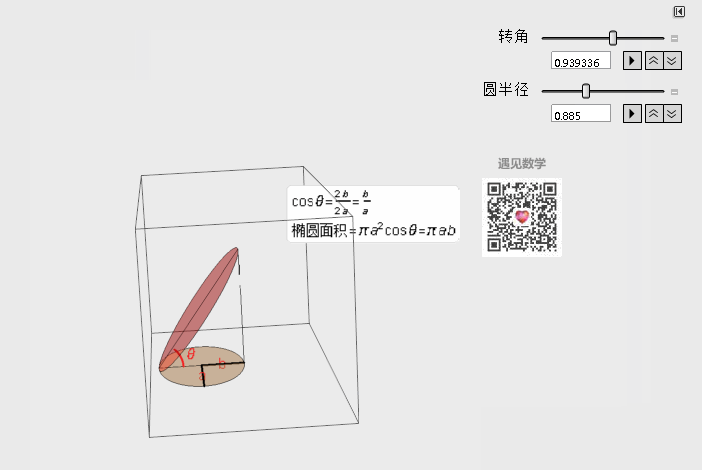
投影的应用--计算椭圆的面积

那下面就看一个很简单的例子 - 求椭圆的面积, 这里我们想象椭圆在三维空间中其实就是由一个圆的投影下来的形状, 有了这个思路就可以用圆的面积乘以它们的余弦夹角, 非常轻松就可以算出来了.

结束语

上面就是利用 Wolfram 语言制作的图解高等数学例子. 好了, 现在让我们在下一篇的中来看一看其他高等数学里相关概念动图.

感谢关注! Thanks!