二元函数的偏导数|文艺数学君

来源

因为曲面上的每一点都有无穷多条切线，描述这种函数的导数相当困难。偏导数就是选择其中一条切线，并求出它的斜率。通常，最感兴趣的是垂直于y轴（平行于xOz平面）的切线，以及垂直于x轴（平行于yOz平面）的切线。

一种求出这些切线的好办法是把其他变量视为常数。

定义

通过上面的来源，我们很容易给出偏导数的定义。

设函数z=f(x,y),(x,y)∈D，若(x_0,y_0 )∈D,且f(x,y_0 )在x_0的某一邻域内有定义，则当极限

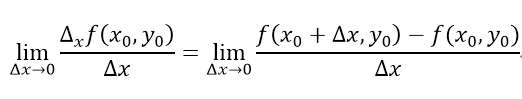
存在时，称这个极限为函数f在(x_0,y_0 )关于x的偏导数∂f/∂x

图形化解释

下面我们来举一个具体的例子，来解释偏导数。

我们考虑函数z=-x^2-y^2在点(0.5,1,-1.25)处的偏导数。要求该点关于x的偏导数可以理解为求z=-x^2-y^2和y=1两个曲面的交线在点(0.5,-1.25)处的切线。求关于y的偏导数可以理解为求z=-x^2-y^2和x=0.5两个曲面的交线在点(1,-1.25)处的切线。

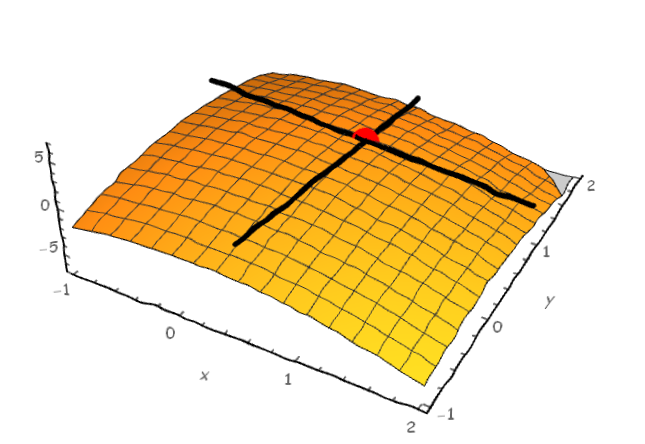
• 首先我们来看一下函数z的图像和点(0.5,1,-1.25)在图中所在的位置

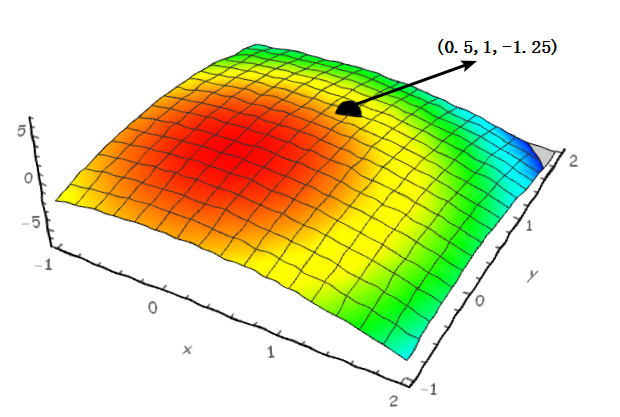
我们做辅助面x=0.5和y=1，一会要在这两个辅助面上分别求切线。

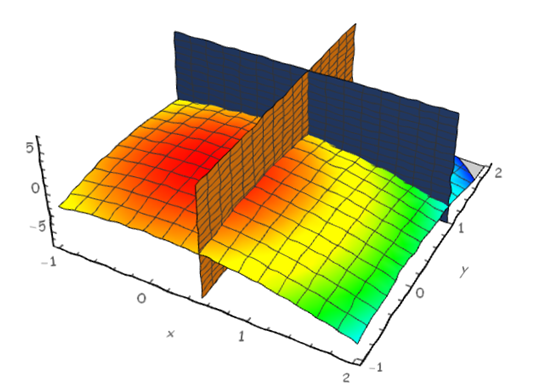
接下来即考虑在辅助面x=0.5上时求出在点(0.5,1,-1.25)处关于y的偏导数和y=1时求出在点(0.5,1,-1.25)处关于x的偏导数

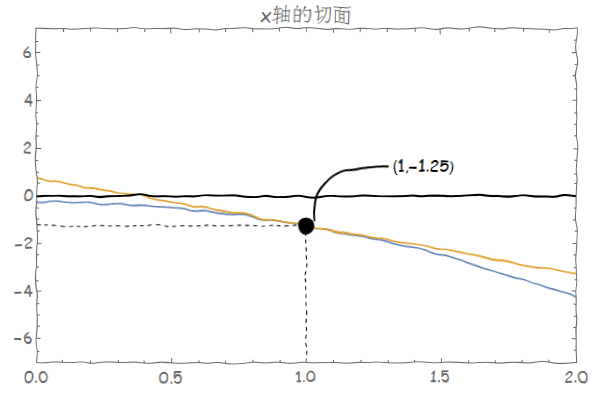
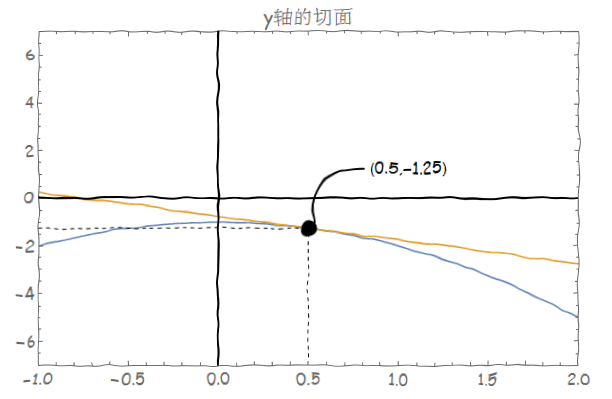
我们把两条切线在三维图像中表示出来。关于三维图中直线的斜率我们可以通过现在辅助面上求出切线上两点，再加上辅助面的值。如辅助面x=0.5的切线维为y=-2(x-1)-1.25，我们取切线上两点为(-1 , 2.75)和(2 , -3.25)，则加上x=0.5，则点是三维图中切线上的两点(0.5 , -1 , 2.75)和(0.5 , 2 , -3.25)，我们既可确定这条切线的位置。

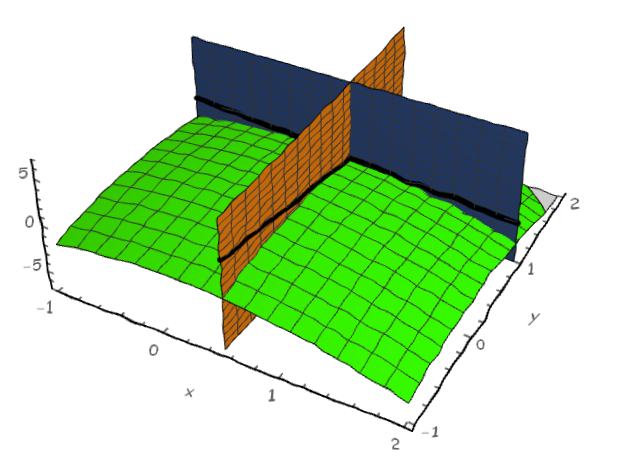
加上辅助面一起展示

我们可以看到辅助面上有黑色的线，那个就是切线。

几何意义

通过上面的图像分析和偏导数来源的讲解，我们可以看出来二元函数实际上就是表示固定面上一点的切线斜率。其中，

• 偏导数f_x (x_0,y_0)表示固定面上一点对x轴的切线斜率；
• 偏导数f_y (x_0,y_0)表示固定面上一点对y轴的切线斜率。

拓展到高阶偏导数：

如果二元函数z=f(x,y)的偏导数f_x (x_0,y_0)(这个表示在x0,y0出的x的偏导数)与f_y (x_0,y_0)仍然可导，那么这两个偏导函数的偏导数称为z=f(x,y)的二阶偏导数。