函数的极限( ε – δ 语句)|文艺数学君

定义

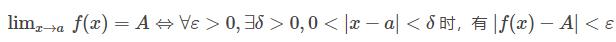
即：任意给定一个大于0的实数ε，若存在以a为中心的空心邻域：

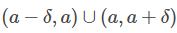
对任意：

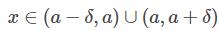
都有x的函数值f(x)与某个定值A的差的绝对值不超过ε，则称f(x)在a的极限为A。

图形化解释

但是上面的定义还是不是很直观，下面我们来举两个例子，分别使用图形来解释一下极限的ε - δ语句。我们会举一个趋于无穷的例子和一个趋于定点a的例子。

趋于无穷的极限

在这里我们举的例子是：

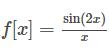
我们要求x趋于无穷时，f[x]的极限。 根据定义中∀ε>0，在这里我们首先取ε = 0.09，我们可以看到∃δ = 10.39，则有x > δ时，有|f(x)|<ε，即|f(x)-0|<ε。

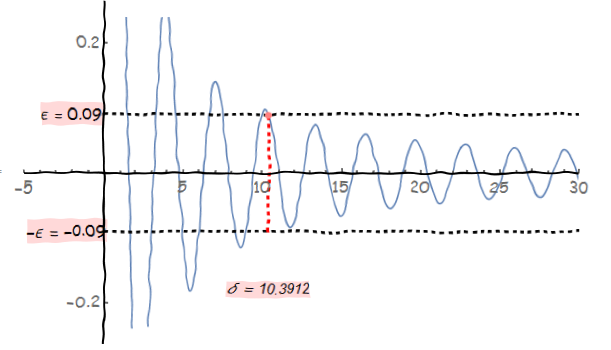
由于是∀ε>0，我们可以再取ε = 0.05，我们可以看到∃δ = 19.71，有x > δ时，则有|f(x)|<ε，即|f(x)-0|<ε。

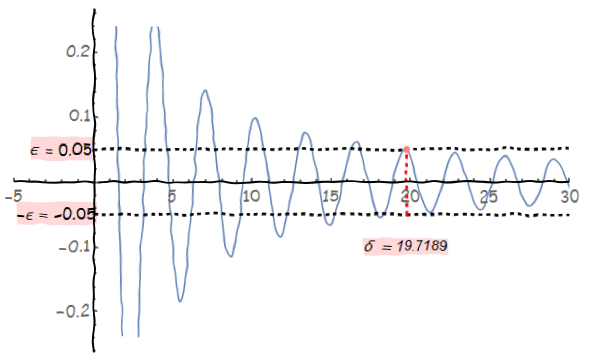
我们可以看到，不管ε取何值，我们都可以找到对应的δ，使得x>δ时，有|f(x)-0|<ε，所以f[x]的极限是0。

趋于点a的极限

我们还是看刚刚那个函数，但是此时我们不让x趋于无穷，而是让x->17，我们来看此时f[x]的极限。 根据定义中∀ε>0，在这里我们首先取ε=0.1，我们可以看到∃δ = 14.90，则有|x-17|<δ时，有|f(x)- f[17]|<ε。

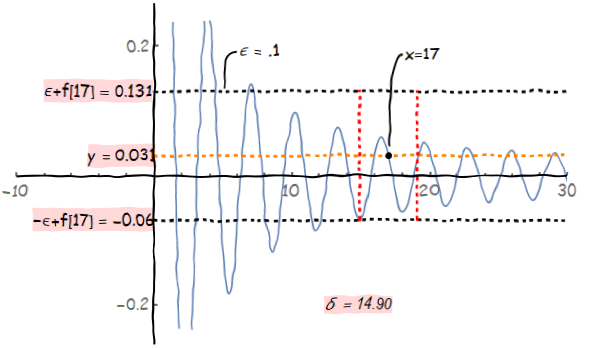
由于是∀ε>0，我们可以再取ε = 0.07，我们可以看到∃δ = 16.47，有|x-17|<δ时，有| f(x) - f[17] |<ε。

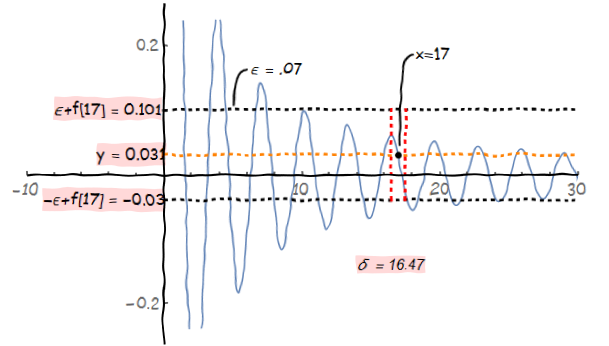
我们可以看到，不管ε取何值，我们都可以找到对应的δ，使得0<|x-17|<δ时，有| f(x) - f[17] |<ε，所以f[x]在x=17时的极限是f[17]（这里f[17]是可以取到的）。

历史

下面我们来说一下ε - δ语句的来历。在牛顿一开始弄微积分的时候，是使用△x来表示小的增量，但是当时的英国主教乔治·贝克莱就批评牛顿的流数观念，比如说在求微分的时候，牛顿首先给出x一个增量△x，然后又让△x是零，这违背了“背反律”，就是说既然开始定义了△x是一个增量，那么△x就不能为0（不然增什么量呢？），然后在求微分时又让△x成为了零，这不是相互矛盾了吗？而这个也演变成了第二次数学危机。

在这次危机的解决过程中，起到关键作用的就是“现代分析之父”——Weierstrass，他在Cauchy和Abel工作的基础上，提出了著名的函数极限“ε-δ”定义，即我们现在所学的极限的严格定义。通过极限概念的提出，我们也意识到在数学分析中的一个重要事实：很多数只能由极限来定义。

历史评价

函数极限的“ε-δ”定义第一次使极限和连续性摆脱了与几何和运动的任何牵连，给出了只建立在数与函数概念上的清晰的定义，从而使一个模糊不清的动态描述，变成为一个严密叙述的静态观念，这不能不认为是变量数学史上的一次重大创新。今天“ε-δ”语言的精髓已经深入到现代数学的每一根血管,牵动着每一根神经。

一个有趣的解释

函数极限的“ε-δ”定义就像孙悟空ε与如来佛δ。

孙悟空ε不管怎么努力，都逃不过如来佛δ的掌心。只要|x－x0|＜δ，则|f(x)－A|＜ε。如来佛δ通过控制自己的大小，可以让孙悟空ε任意的小。