极坐标-图解高等数学20

概述

• 文章转自：微信号 meetmath
• 由@文艺数学君@王茂南整理修订并发布

图解高等数学系列, 是以动图的形式将的数学知识点展示出来.

希望该系列能够帮助朋友更加深刻的理解某些较为抽象的概念. 也因为本人水平有限, 疏忽错误在所难免, 所以还请各位老师和朋友不吝赐教, 多提宝贵意见, 帮助我改进这个系列, 先感谢感谢啦!

这一篇文章会简单介绍极坐标的相关内容并作出可视化的解释.

极坐标

坐标系只是人们描述空间任意位置的一种方法, 除了笛卡尔坐标系, 最常见到的还有极坐标系, 有时候用极坐标来表示函数会更简洁, 甚至对某些曲线而言, 只有极坐标能够表示.

极坐标中的点

极坐标系也有两个坐标轴: r (极径)和θ (极角或角坐标), r表示到极点的距离, θ表示旋转的角度. 有了r和θ之后, 也可以描述二维平面上的任何位置.

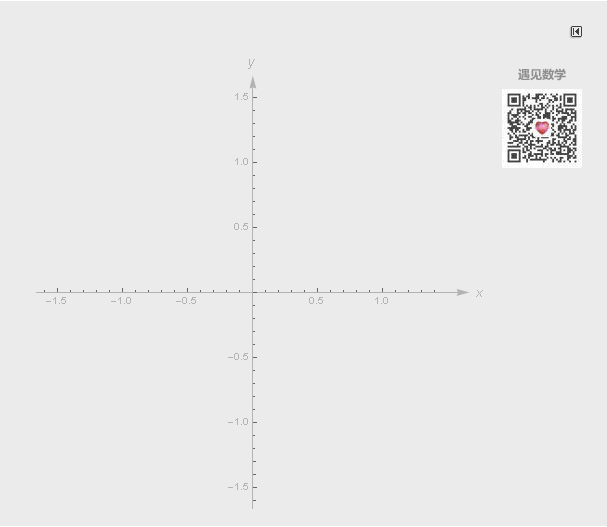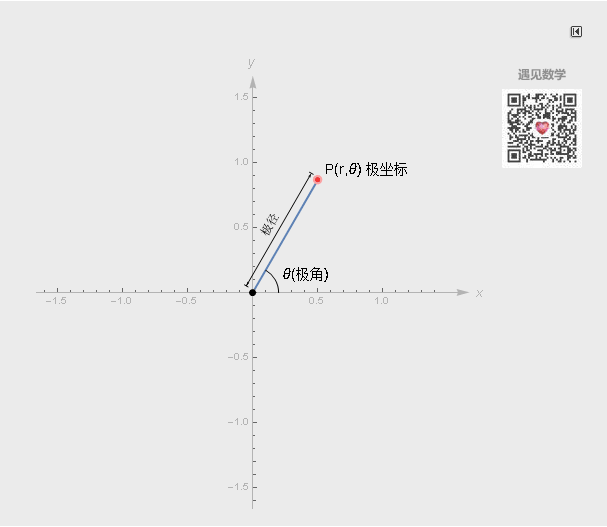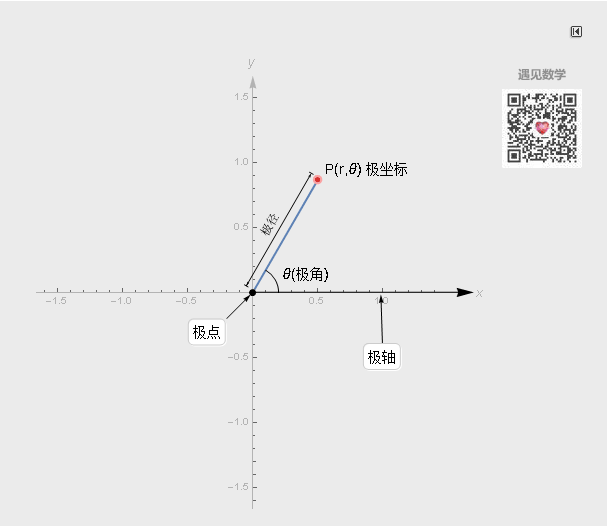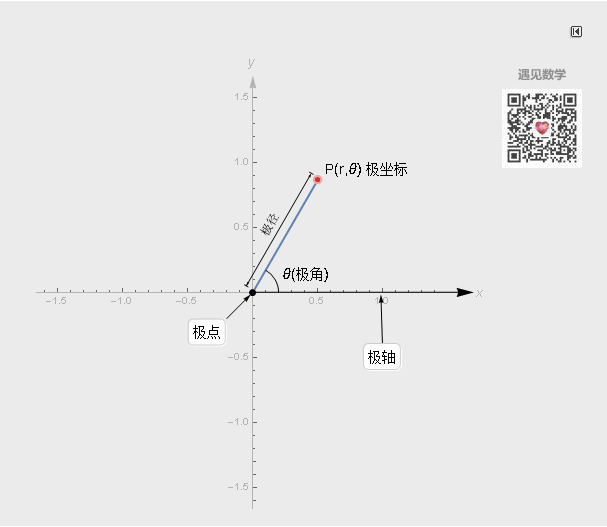
极坐标系中一个重要的特性是, 平面直角坐标中的任意一点, 可以在极坐标系中有无限种表达形式. 通常来说, 点(r, θ)可以任意表示为(r, θ±n×360°)或(−r, θ±(2n + 1)180°)

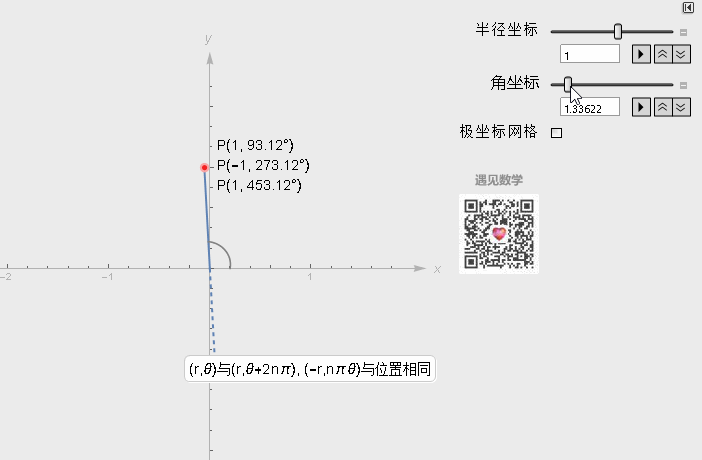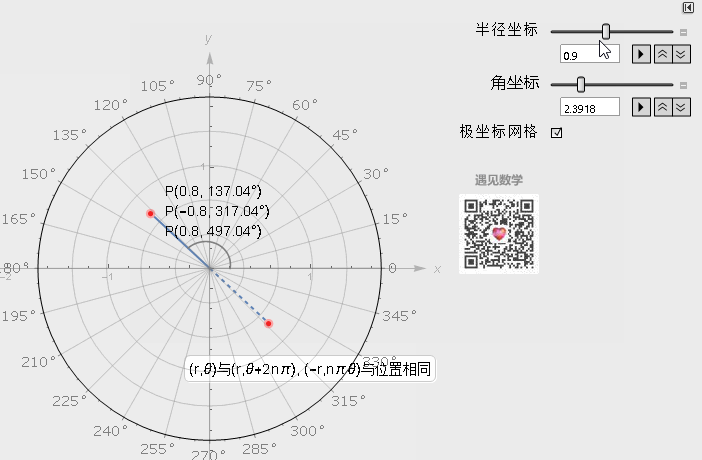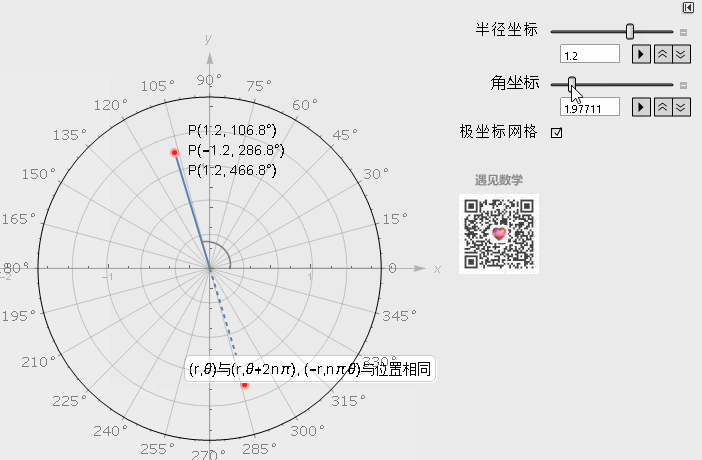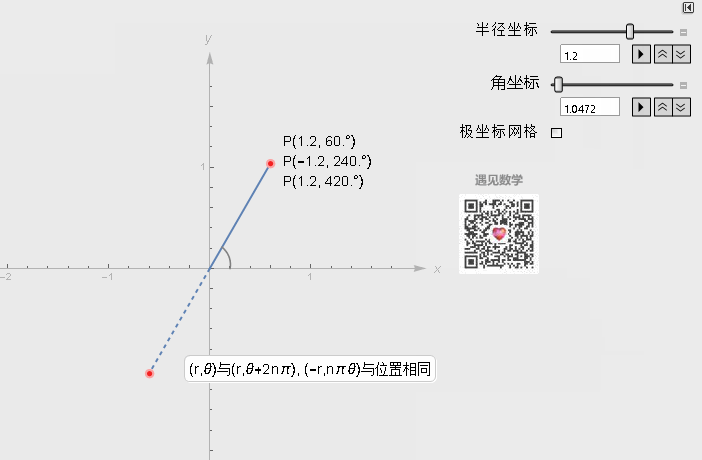
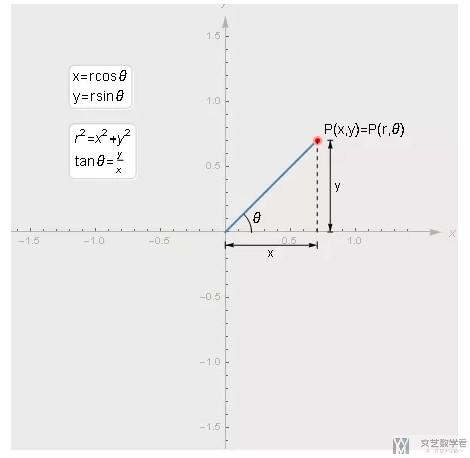
与笛卡尔坐标系的转换

从极坐标r和θ可以变换为笛卡尔直角坐标系, 当然也可以从直角坐标x和y也可以变换为极坐标：

曲线的极坐标表示

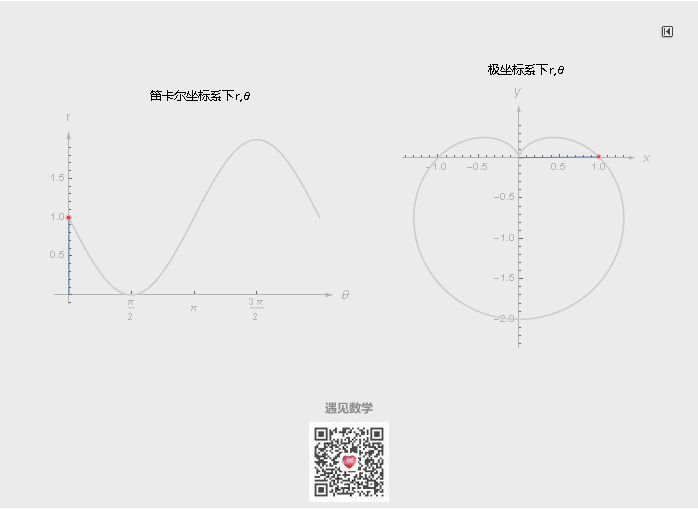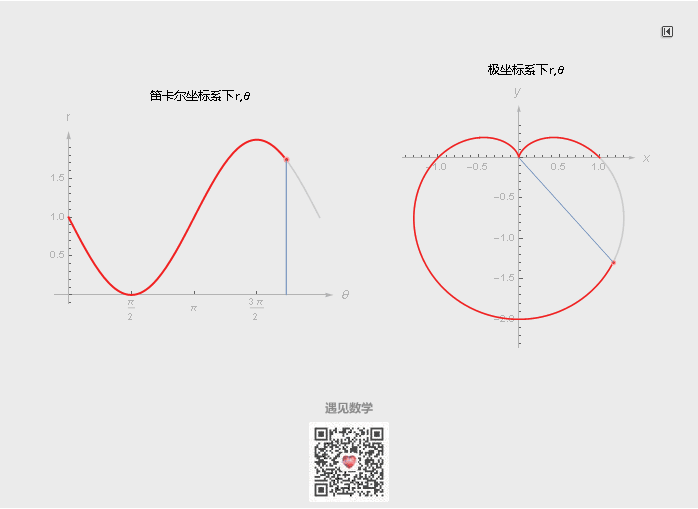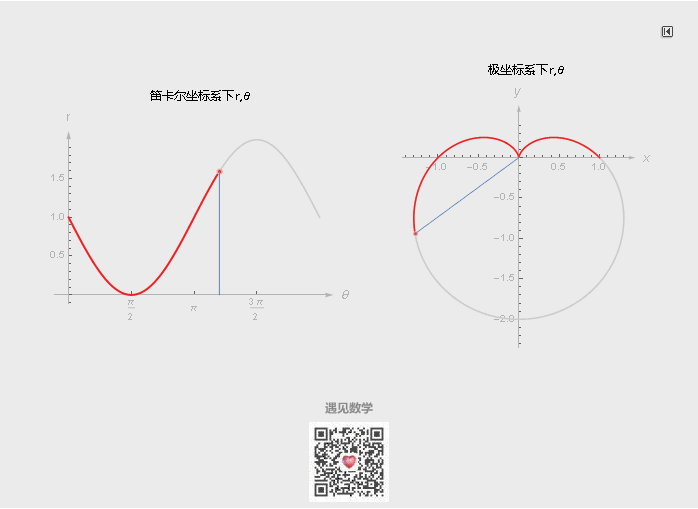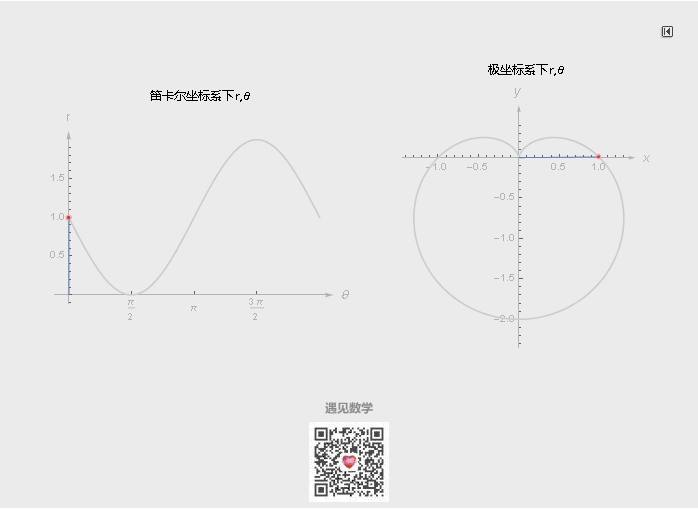
平面上的曲线也可以由极坐标来表示, 很多非常著名的几何图案(心脏线)都是用极坐标来表示, 反过来如果用笛卡尔坐标系来做就会显得非常繁杂. 看下面在极坐标系下 1 - Sinθ 的图形以及在直角坐标系下是如何改变的:

对数螺线(等角螺线), 在极坐标系(r, θ)中，这个曲线可以写为:

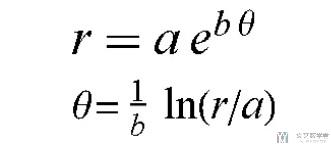
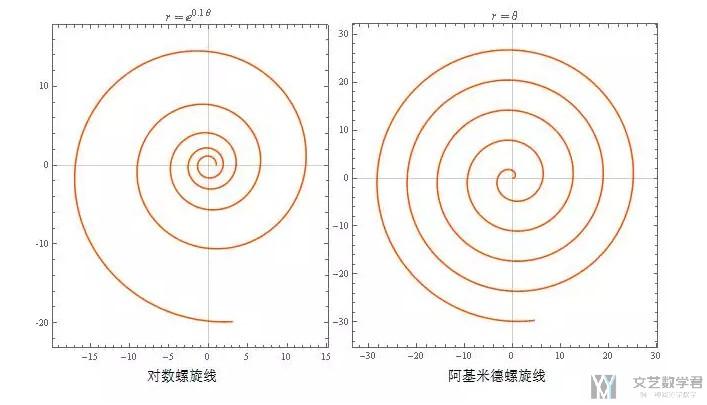
著名的数学家雅各布·伯努利发现了将对数螺旋线做放大或缩小, 均能与原曲线重合. 在惊叹这曲线之余, 决定将对数螺旋线作为自己的墓志铭 - "纵使变化，依然故我"(eadem mutata resurgo).  不过制作墓碑的石匠因为不懂数学, 最终竟将阿基米德螺旋线雕刻上去了.(见图片下部所示, 图自网络)

我们也来对比下这两种曲线:

结束语

上面就是利用 Wolfram 语言制作的图解高等数学例子. 好了, 现在让我们在下一篇的中来看一看其他高等数学里相关概念动图.

感谢关注! Thanks!