文章目录(Table of Contents)
简介
这一篇介绍四种Norm的方式. 之前我们介绍过BatchNorm的方法, Batch Normalization技术介绍. 这一篇会将BatchNorm, LayerNorm, InstanceNorm和GroupNorm这四种Normailzation的技术一起进行比较和说明.
参考资料
- Pytorch Normalization Layers(官方文档使用说明): Normalization layers
- Pytorch Normalization中文介绍: ytorch常用normalization函数
- 下面大图的来源(Twitter上的一张图片): Summary and visualization of different normalization techniques
四种Normalization方式介绍
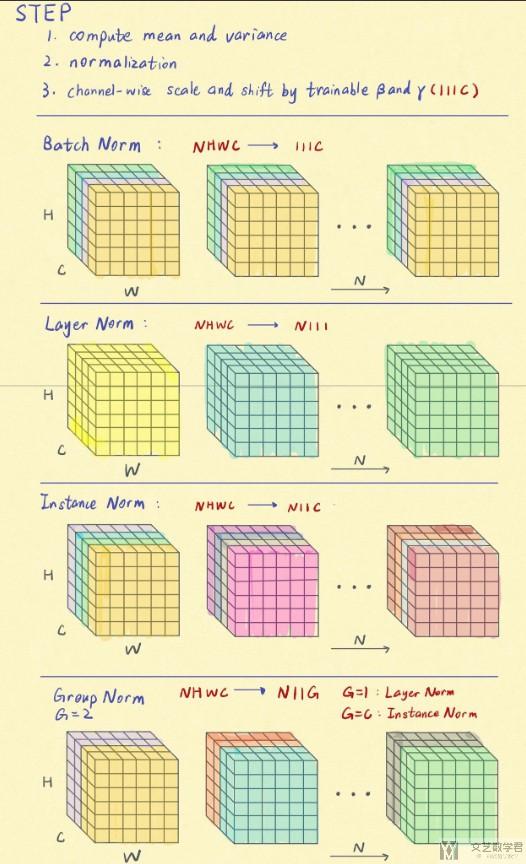
下图是四种Normalization方式的一个汇总(我个人感觉这个图看起来方便一些).
- 图中每一个正方体块表示一个数据(比如说这里一个正方体就是一个图像)
- 每一个正方体中的C, H, W分别表示channel(通道个数), height(图像的高), weight(图像的宽)
- 下图介绍了4中Norm的方式, 如Layer Norm中NHWC->N111表示是将后面的三个进行标准化, 不与batch有关.
- 我们可以看到, 后面的LayerNorm, InstanceNorm和GroupNorm这三种方式都是和Batch是没有关系的.
下面我们使用一个(2, 2, 4)的数据来举一个例子, 我们可以将其看成有2个图像组成的单通道的图像.
生成测试使用数据
我们首先生成测试使用的数据, 数据的大小为(2, 2, 4);
- x_test = np.array([[[1,2,-1,1],[3,4,-2,2]],
- [[1,2,-1,1],[3,4,-2,2]]])
- x_test = torch.from_numpy(x_test).float()
- x_test
- """
- tensor([[[ 1., 2., -1., 1.],
- [ 3., 4., -2., 2.]],
- [[ 1., 2., -1., 1.],
- [ 3., 4., -2., 2.]]])
- """
测试LayerNorm与GroupNorm
关于这里的计算的细节, 会在后面的计算细节描述部分进行叙述. 这里就看一下如何使用Pytorch来进行计算, 和最终计算得到的结果.
LayerNorm就是对(2, 2, 4), 后面这一部分进行整个的标准化. 可以理解为对整个图像进行标准化.
- m = nn.LayerNorm(normalized_shape = [2,4])
- output = m(x_test)
- output
- """
- tensor([[[-0.1348, 0.4045, -1.2136, -0.1348],
- [ 0.9439, 1.4832, -1.7529, 0.4045]],
- [[-0.1348, 0.4045, -1.2136, -0.1348],
- [ 0.9439, 1.4832, -1.7529, 0.4045]]], grad_fn=<AddcmulBackward>)
- """
当GroupNorm中group的数量是1的时候, 是与上面的LayerNorm是等价的.
- # Separate 2 channels into 1 groups (equivalent with LayerNorm)
- m = nn.GroupNorm(num_groups=1, num_channels=2, affine=False)
- output = m(x_test)
- output
- """
- tensor([[[-0.1348, 0.4045, -1.2136, -0.1348],
- [ 0.9439, 1.4832, -1.7529, 0.4045]],
- [[-0.1348, 0.4045, -1.2136, -0.1348],
- [ 0.9439, 1.4832, -1.7529, 0.4045]]])
- """
测试InstanceNorm和GroupNorm
InstanceNorm就是对(2, 2, 4), 标红的这一部分进行Norm.
- m = nn.InstanceNorm1d(num_features=2)
- output = m(x_test)
- output
- """
- tensor([[[ 0.2294, 1.1471, -1.6059, 0.2294],
- [ 0.5488, 0.9879, -1.6465, 0.1098]],
- [[ 0.2294, 1.1471, -1.6059, 0.2294],
- [ 0.5488, 0.9879, -1.6465, 0.1098]]])
- """
上面这种InstanceNorm等价于当GroupNorm时num_groups的数量等于num_channel的数量.
- # Separate 2 channels into 2 groups (equivalent with InstanceNorm)
- m = nn.GroupNorm(num_groups=2, num_channels=2, affine=False)
- output = m(x_test)
- output
- """
- tensor([[[ 0.2294, 1.1471, -1.6059, 0.2294],
- [ 0.5488, 0.9879, -1.6465, 0.1098]],
- [[ 0.2294, 1.1471, -1.6059, 0.2294],
- [ 0.5488, 0.9879, -1.6465, 0.1098]]])
- """
计算细节描述
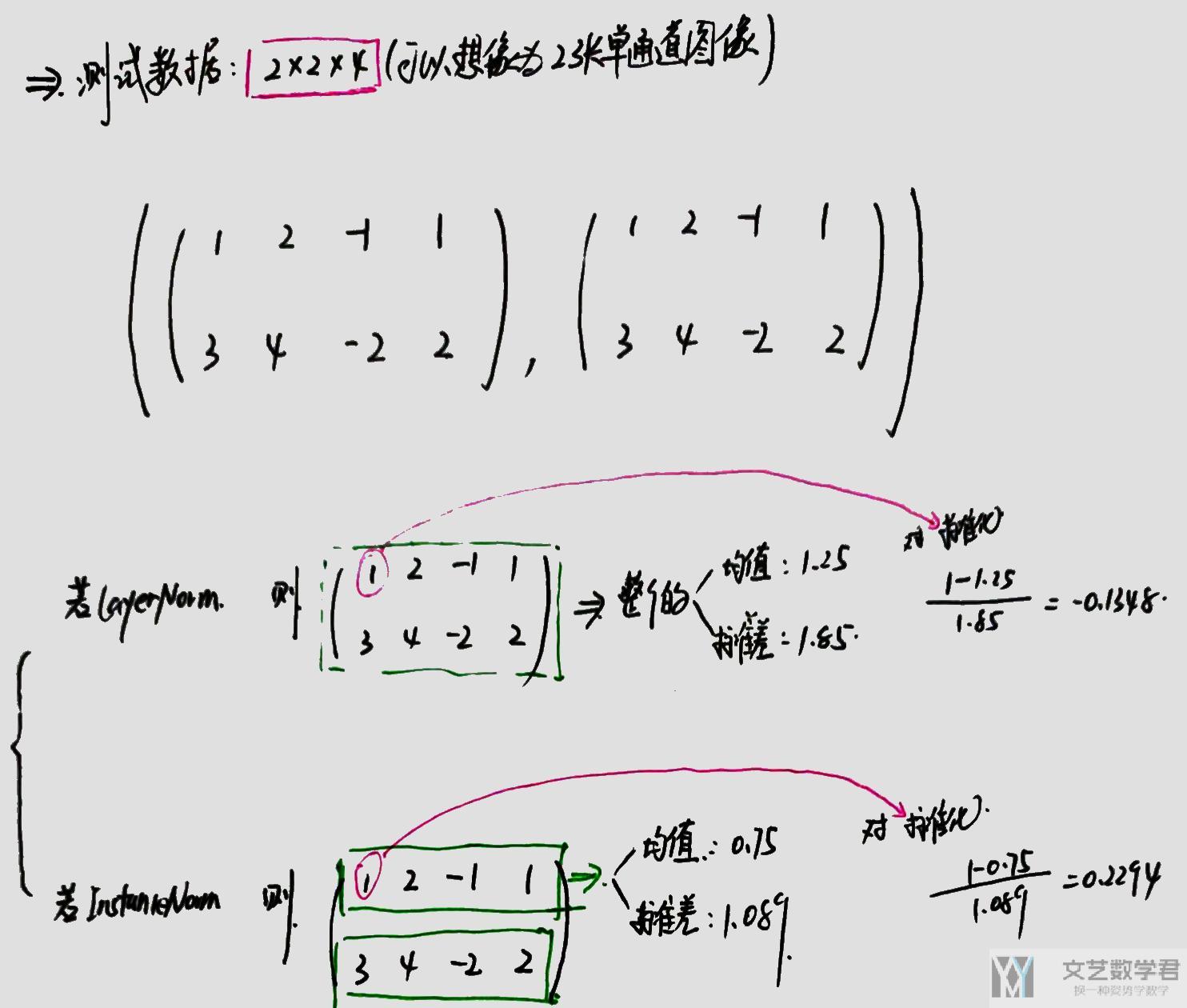
我们看一下在上面的LayerNorm和InstanceNorm中的结果是如何计算出来的. 我们只看第一行第一列的数据1进行标准化的过程. 下面是详细的计算的过程(这里的计算结果与上面直接计算的结果是相同的).
每一种方式适合的场景
这里我也是没有自己测试过, 就先放一下我看到的别人写的内容.
- batchNorm是在batch上,对小batchsize效果不好;
- layerNorm在通道方向上,主要对RNN作用明显;
- instanceNorm在图像像素上,用在风格化迁移;
- GroupNorm将channel分组,然后再做归一化, 在batchsize<16的时候, 可以使用这种归一化;
- 微信公众号
- 关注微信公众号
-

- QQ群
- 我们的QQ群号
-













评论