Pytorch入门教程08-激活函数介绍

简介

上一篇我们主要讲了线性回归问题. 但是, 有很多问题不是线性函数可以解决的, 这个时候需要引入了激活函数来解决非线性的问题.

这一篇主要介绍常见的激活函数, 和相应的函数图像.

• Sigmoid函数, 函数的范围为(0,1).
• ReLU函数, 函数的范围为(0,+无穷).
• Tanh函数, 函数的范围为(-1,1).

常见激活函数可视化

Sigmoid函数

Sigmoid函数(又名Logistic函数), 他是深度学习中最经典的, 最先被使用的激活函数之一, 他可以将数据压缩到[0,1]的范围里. 在Pytorch中, 可以通过nn.Sigmoid()来进行使用. 他的公式如下所示:

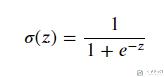
我们绘制出该函数的图像.

Sigmoid函数的图像如下图所示:

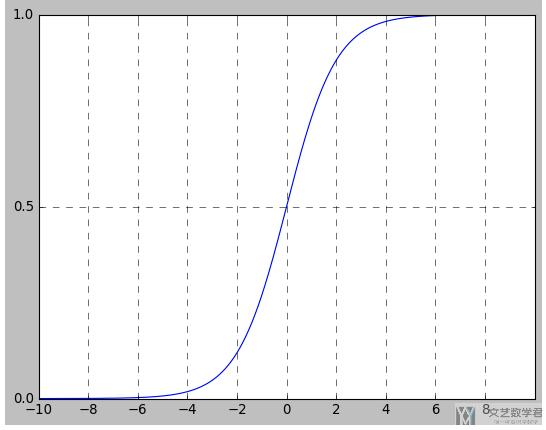
从上图中, 激活函数Sigmoid在定义域内处处可导(平滑的). 但是, 通过曲线的斜率, 可以发现, 当输入一个较小或较大的数时, 该函数的导数会变得很小, 梯度趋近于0. 当经过多次导数之后, 梯度就会变得很小, 出现梯度消失的问题.

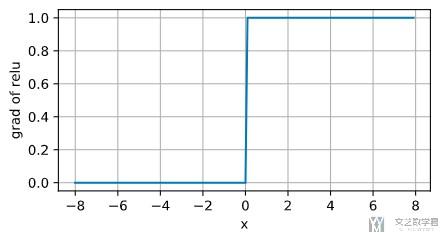
我们对Sigmoid进行求导, 梯度为下面的表达式.

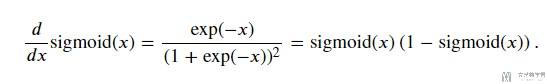
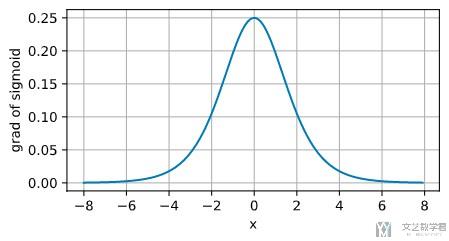
我们将画出上面梯度的函数, 从下图可以看到:

• 当x=0的时候, 梯度达到最大, 此时是0.25.
• 当x向0的左右两边移动的时候, 梯度减小, 逐渐变为0.

关于更多梯度消失, 可以查看链接: 梯度消失解释

Tanh 函数

Tanh是双曲函数中的双曲正切函数, 他的数学公式如下所示, 他可以将数据压缩到[-1,1]的范围里:

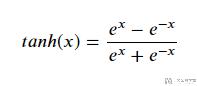
接着绘制出Tanh的函数图形:

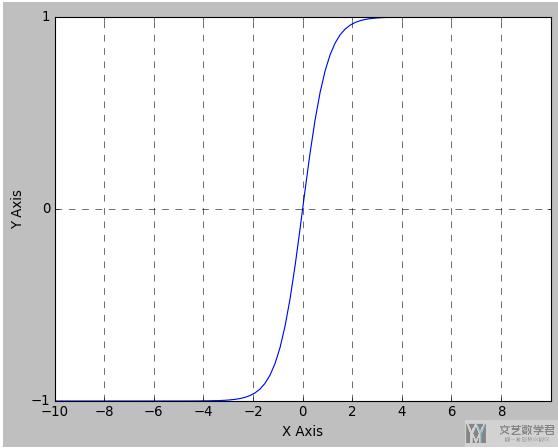
Tanh的函数图像如下所示:

同样, Tanh的导数如下所示:

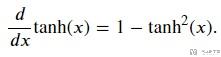
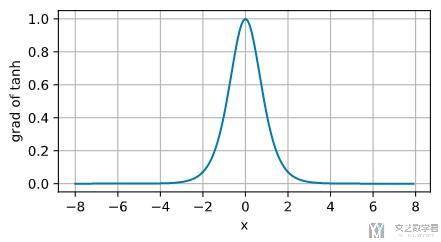
我们对其进行可视化, 可以看到:

• 在x=0的地方, tanh的导数达到最大, 此时是1;
• 在0的周围, 导数逐渐减小;

ReLU函数

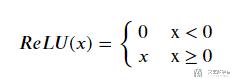Tanh(双曲正切函数)和Sigmoid函数相似, 也存在着梯度消失现象. 且由于解析式中存在幂运算, 计算起来较复杂. 因此, 为了解决梯度消失的问题, 线性修正单元函数(Rectified Linear Units，简称ReLU)孕育而生. ReLU是目前比较常用的激活函数之一. ReLU公式如下所示: 接着我们绘制出ReLU的函数图像:

1. def relu(x):
2.     return np.where(x >= 0, x, 0)
5. y = np.linspace(-3, 3, 100)
6. plt.plot(y, relu(y), 'b')
7. plt.grid(linestyle='--')
9. plt.xticks(np.arange(-3,4,1))
10. plt.yticks([0, 1, 2, 3])
11. plt.ylim(0, 3)
12. plt.xlim(-3, 3)
13. plt.show()

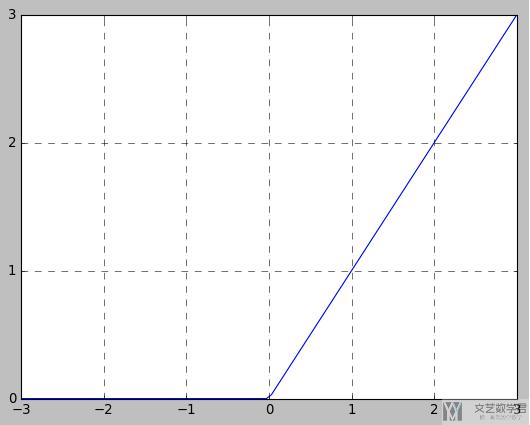ReLU的图像为: 接着, 我们绘制出ReLU的梯度, 可以看到他的梯度表现是很好的, 减轻了梯度消失的问题. 下面是绘制梯度的代码, 因为我们要绘制每个x的梯度值, 所以我们在反向传播的时候需要传入一个相同大小的向量, 相当于进行求和操作.

1. x = torch.arange(-8.0, 8.0, 0.1, requires_grad=True)
2. y = torch.relu(x)
3. y.backward(torch.ones_like(x), retain_graph=True)
4. plot(x.detach(), x.grad, 'x', 'grad of relu', figsize=(5, 2.5))

最终ReLU的梯度图像如下所示:

关于梯度爆炸与梯度消失

梯度消失

最常见导致梯度消失的原因是激活函数的选择. 激活函数会随着线性层的变多而变多. 例如, 若我们使用sigmoid来作为激活函数, 他的梯度如下图所示:

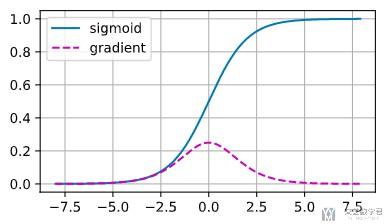
可以看到, 当输入x过大或是过小的时候, sigmoid的梯度都会变小. 当反向传播经过多层之后, 多次结果相乘, 最终梯度会变得很小. 正是因为Sigmoid存在这样的问题, 所以ReLU才会开始使用.

梯度爆炸

梯度爆炸可能是由于我们网络参数的初始化不好. 例如下面都是从均值为0, 方差为1的高斯分布进行采样, 并进行矩阵相乘. 我们这样相乘100次 (可以理解为正向传播的时候, 过了100层), 可以看到最终结果会很大.