参数估计之区间估计

摘要

介绍经典的对于正态总体参数的区间估计方法并使用mathematica进行模拟实现。

区间估计：

度量一个点估计的精度的最直观方法就是给出未知参数的区间，此即是区间估计。

置信区间：

设θ是总体的一个参数，x1,x2,...,xn是来自该总体的样本，对于一个给定的置信水平α（0<α<1），假设有两个统计量θ1，θ2，它们都是样本的函数，若对在θ的参数空间中的任何一个值，都有P(θ1≤θ≤θ2)≥1-α，则称随机区间[θ1，θ2]为θ的置信水平为1-α的置信区间。

说明：求置信区间的方法主要是枢轴量法，枢轴量法有以下三步

1. 设法构造一个样本和θ的函数G，使得其分布不依赖于未知参数，称其为枢轴量。
2. 适当的选取两个常数c,d，使得对给定的α有P（c≤G≤d）=1-α。（离散场合改为≥α）
3. 假如能将c≤G≤d进行不等式等价变形成为θ1≤θ≤θ2，则[θ1，θ2]是θ的1-α置信区间。

 

现主要讨论正态总体情况下的区间估计。

下面会用到一些抽样分布的知识，一些基础知识可以看下面的链接：

三大抽样分布总结

关于求置信区间的例子，可以看一下这个链接：

区间估计习题

 

一、单个正态总体参数的区间估计

1.σ未知时μ的置信区间

枢轴量：

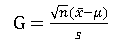
1-α置信区间：

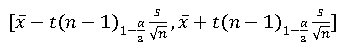
下面看一下mathenatica实现：

 

2.σ已知时μ的置信区间

枢轴量：

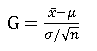
1-α置信区间：

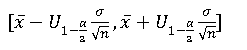
mathenatica实现：

 

3.σ^2的置信区间

 

枢轴量：

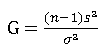
1-α置信区间：

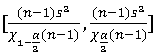
mathematica实现：

 

二、双正态总体参数的区间估计

 

1.σ1^2和 σ2^2均已知时，μ1-μ2的区间估计

枢轴量：

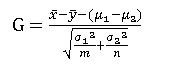
1-α置信区间：

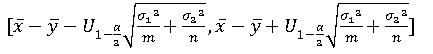
mathematica实现：

 

2.σ1^2和 σ2^2未知但相等时，μ1-μ2的区间估计

枢轴量：

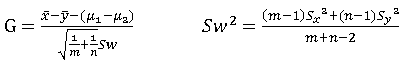
1-α置信区间：

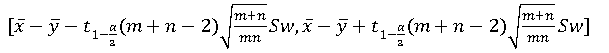
mathematica实现：

 

3.σ1^2/ σ2^2的区间估计

枢轴量：

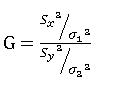
1-α置信区间：

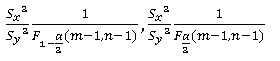
mathematica实现：

 

三、其他可行函数

在使用下面的函数之前，去要先导入函数包,Needs["HypothesisTesting`"]

1.NormalCI

对于单正态总体方差已知时均值的区间估计，还可以用函数NormalCI估计，NormalCI是在分布标准差已知，由样本平均值来求正态总体数学期望的置信区间，它的参数依次需要样本均值，总体期望的标准差。

结果和“一”中的一样

 

2.StudentTCI

 

对于单正态总体方差未知时的均值的区间估计，还可以用函数StudentCI估计，它由样本平均值和样本标准差来求总体数学期望的置信区间，它的参数依次需要样本均值，样本的标准差以及自由度，因为是利用t分布求解，所以自由度为数据个数减一，即100-1=99。

 

结果和“一”中的一样

 

3.ChiSquareCI

对于单正态总体方差的区间估计可以使用ChiSquareCI，它使用总体方差的无偏估计以及自由度来求总体方差的置信区间。

 

4.FRatioCI

对于双正态总体方差比值的区间估计可以使用FRatioCI，它使用两个总体方差之比以及各自数据个数来求方差比值的置信区间。

 

结果和“二”中相近，略有差别因为比例的小数位保留不一样