导数与微分-图解高等数学08

前言

• 文章转自：微信号 meetmath
• 由@文艺数学君@王茂南整理修订并发布

图解高等数学系列, 是以动图的形式将的数学知识点展示出来.

希望该系列能够帮助朋友更加深刻的理解某些较为抽象的概念. 也因为本人水平有限, 疏忽错误在所难免, 所以还请各位老师和朋友不吝赐教, 多提宝贵意见, 帮助我改进这个系列, 先感谢感谢啦!

导数(Derivative)

导数反映函数变化的快慢程度. 看下面的例子, 比如从家开车出发, 往右边超市行驶. 最下的图形蓝色曲线表示行驶的路程和时间, 橙色为速度与时间函数关系.

开始汽车速度会逐步提高, 当然行驶的距离随之增大, 到了时间等于2.4, 因为快要到达超市, 速度减慢到 0(时间为 3.2),  然后开始返程, 行驶距离减小.

开车回去的速度要比来时候要快, 所以橙色曲线在(3.2, 4.3)内要下降的更快些(为负是因为速度方向相反), 时间等于 4.3 , 因为快到家了, 速度开始减慢, 然后直至为0.

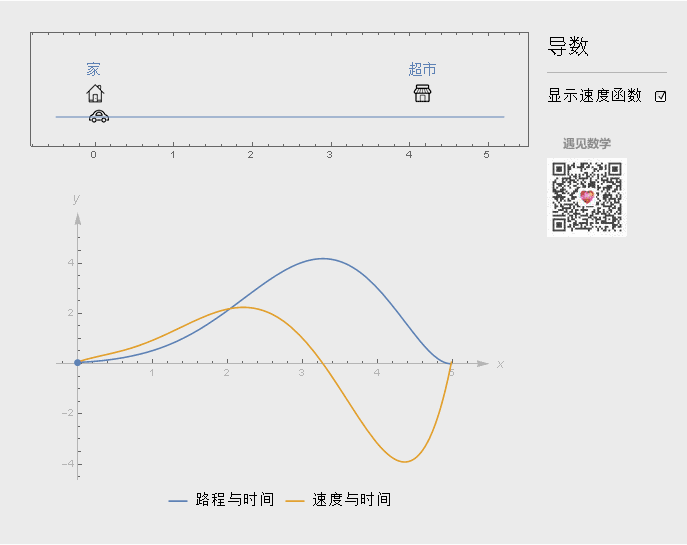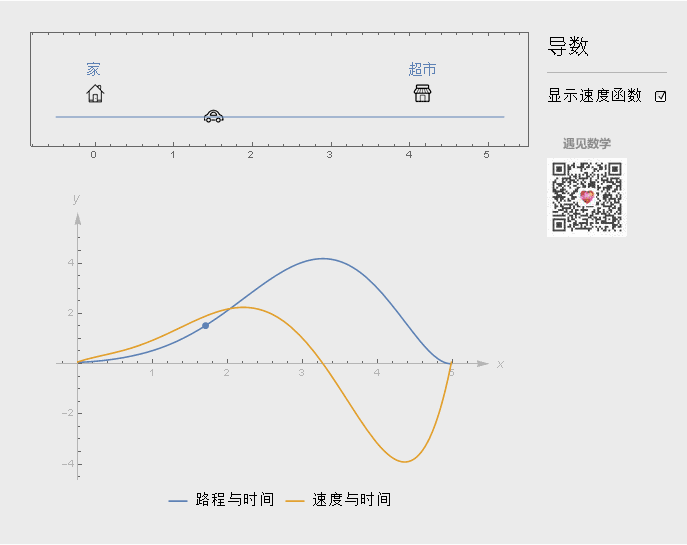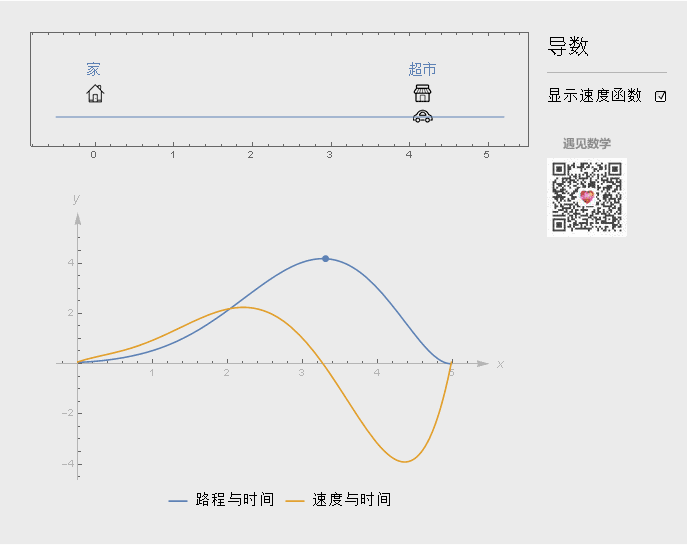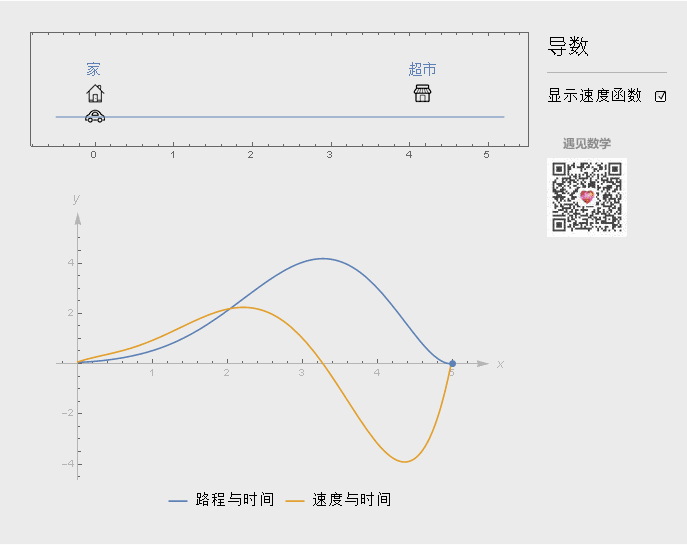
在几何上, 导数即函数某点的切线斜率值, 从图形上来看就是割线上两个点越来越靠近时候(马上与切线重合) △y/△x的比值 .

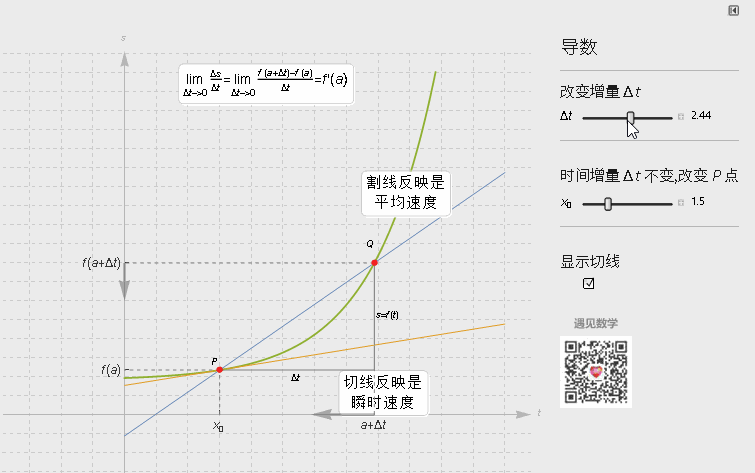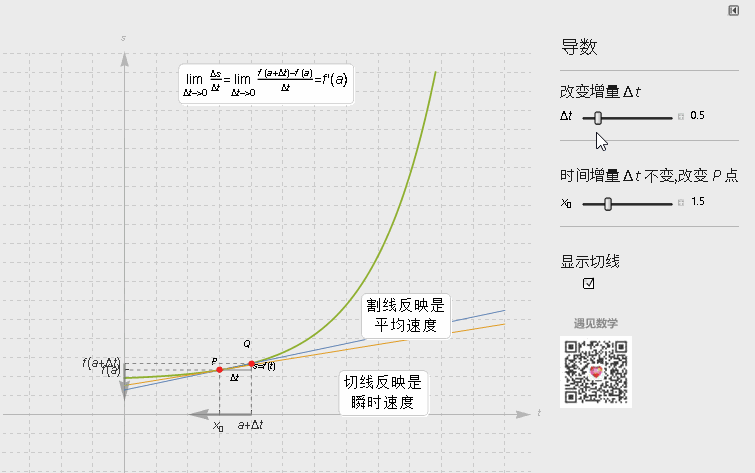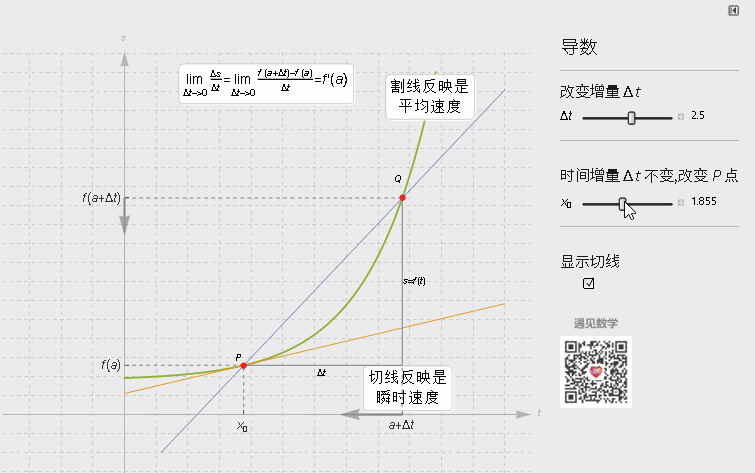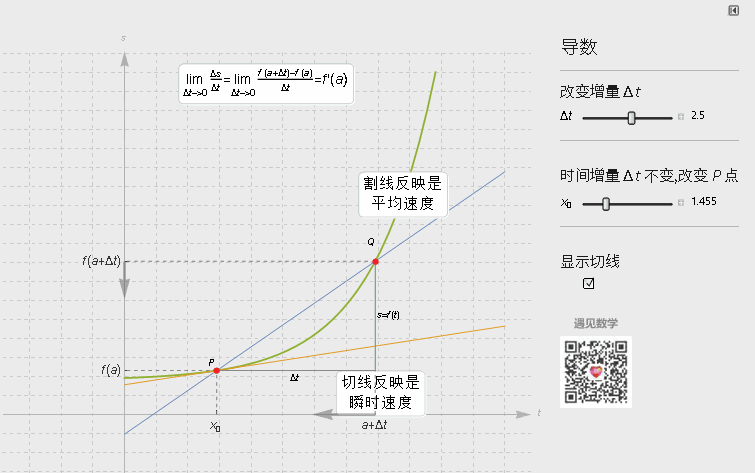
数学上严格的定义, 就需要用极限 ε-δ语言来证明.

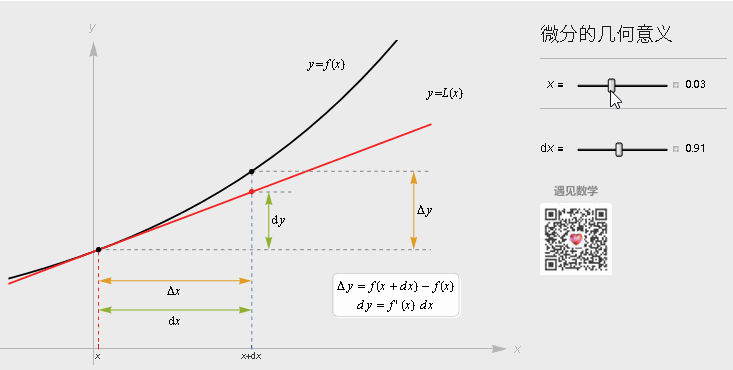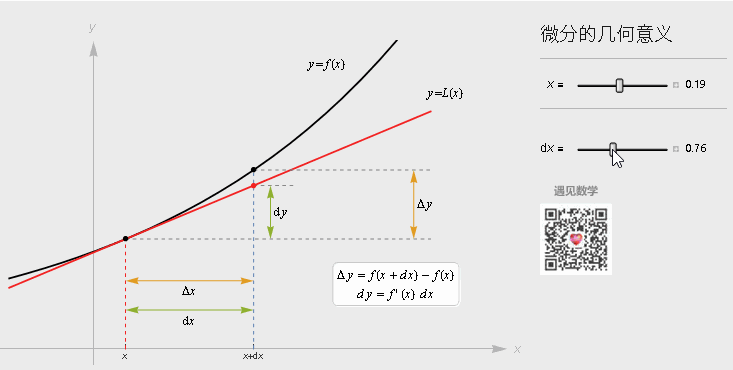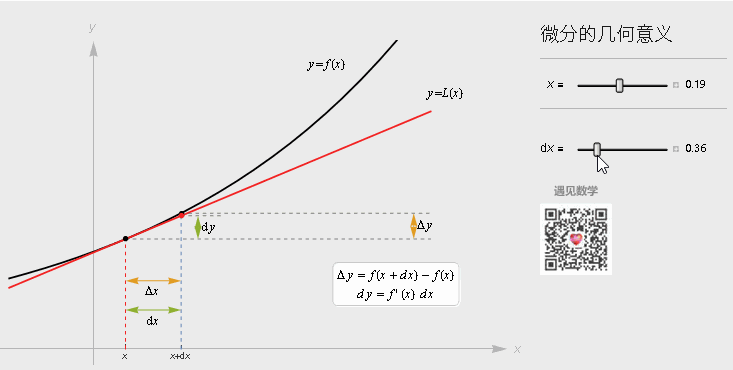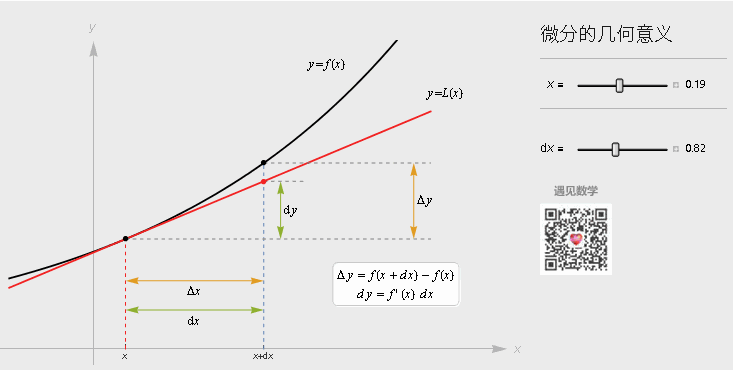
微分

微分就是下图的 d y , 直接见图:

结束语

上面就是利用 Wolfram 语言制作的图解高等数学例子. 好了, 现在让我们在下一篇的中来看一看其他高等数学里相关概念动图.

感谢关注! Thanks!