文章目录(Table of Contents)
简介
Pytorch可以对神经网络进行梯度下降并优化网络的参数. 但同时, 对于普通的优化问题, 我们也可以使用Pytorch来进行解决. 即我们也可以利用梯度下降的思路来寻求最优解.
这一篇文章, 会给出一个简单的例子, 来介绍使用Pytorch来手动进行参数的优化.
关于具体的应用, FunkSVD算法, 我们已经在, 基于矩阵分解的协同过滤, 中进行来叙述. 其实相关的代码也是在那里叙述过了, 我们就不再这里过多的叙述了.
Pytorch解决普通优化问题
下面我们手动的使用Pytorch, 来进行梯度下降, 优化参数, 得到最优解. 我们看下面一个简单的例子(这个例子来自于下面的参考链接, 参考了部分内容, 但进行了修改).
下面是一个简单的线性回归的问题, 我们用Pytorch来解出参数w和b.
- import torch
- import torch.optim as optim
- from torch.autograd import Variable
- w = Variable(torch.randn(3, 5), requires_grad=True) # 这里变量的定义需要注意, 是需要梯度的
- b = Variable(torch.randn(3), requires_grad=True)
- x = Variable(torch.randn(5))
- y = Variable(torch.randn(3))
- optimizer = optim.SGD([w,b], lr=0.01) # 我们要优化的是w和b两个参数
- num_epochs = 100
- for epoch in range(num_epochs):
- optimizer.zero_grad()
- y_pred = torch.mv(w, x) + b # torch.mv表示矩阵与向量相乘
- loss = ((y_pred-y)**2).sum()
- loss.backward()
- optimizer.step()
- if epoch % 5 == 0:
- print(loss)
- y_pred = torch.mv(w, x) + b
- print('y: \n', y)
- print('y_pred: \n', y_pred)
最终我们获得了如下的结果, 可以看到我们最终还是很好的求出了w和b的取值.

参考资料: Manually feeding trainable parameters to the optimizer
一些其他操作
矩阵转置
- pt_matrix_ex # 原始矩阵
- pt_matrix_ex.t() # 转置后的矩阵
参考资料: Transpose A Matrix In PyTorch
矩阵相乘
在Pytorch中, 我们使用torch.mm(a,b)来完成矩阵a和矩阵b的相乘. 比如我们希望矩阵P和矩阵Q的转置相乘, 我们就可以写成下面的这个样子.
- torch.mm(P, Q.t())
关于矩阵相乘, 参考资料: Pytorch中的矩阵相乘
矩阵与向量相乘
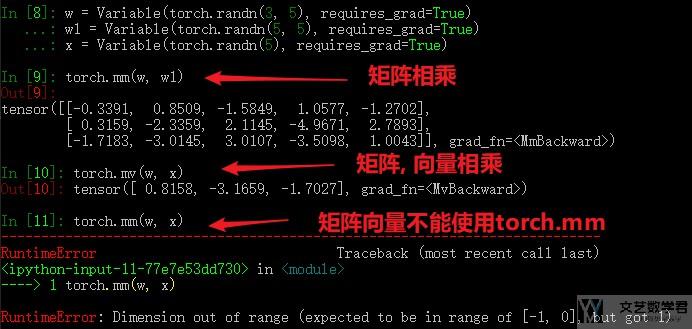
关于矩阵与向量相乘使用torch.mv来进行运算. 与矩阵相乘的区别可以看下面的例子.
- 微信公众号
- 关注微信公众号
-

- QQ群
- 我们的QQ群号
-













评论