PyTorch使用记录02

王 茂南
王 茂南
王 茂南
2827
文章
75
评论
2019年6月14日07:59:21
评论 13325字阅读44分25秒
摘要这一篇文章主要记录一下Pytorch在日常使用中，我经常使用到的一些功能，主要是一个记录的功能。这是第二篇了，上一篇内容有些多了，就再开一篇进行记录。

前言

这一部分是关于PyTorch的一些使用记录，自己经常使用的一些功能会记录在这里，方便自己的查找与使用。(建议直接使用Ctrl+F来进行查找)

这是第二篇关于PyTorch的使用记录了，第一篇的链接，PyTorch使用记录。第一篇有点太长了，所以就在这一篇进行接着记录。

Pytorch动态调整学习率

基本的动态调节

有的时候，我们需要在训练的初始的时候, 将学习率设置的大一些，之后随着训练的进行，逐渐减小学习率，这个时候就需要使用optim.lr_scheduler. 下面是一个简单的例子。

我们需要注意的是，每一个epoch都需要使用exp_lr_scheduler.step().

  1. from torch.optim import lr_scheduler
  3. test_optimizer = optim.SGD([torch.randn(1, requires_grad=True)], lr=1e-3)
  4. exp_lr_scheduler = optim.lr_scheduler.StepLR(test_optimizer, step_size=3, gamma=0.5)
  6. for epoch in range(1, 12):
  7.     exp_lr_scheduler.step() # 要每一个epoch都要使用
  8.     print('Epoch {}, lr {}'.format(
  9.         epoch, test_optimizer.param_groups[0]['lr']))

上面的是每3个epoch，lr都会乘0.5(gamma)PyTorch使用记录02

于是，我们在绘制loss函数图像的时候，可以看到下面这种效果, 每次lr减小后loss能继续下降.

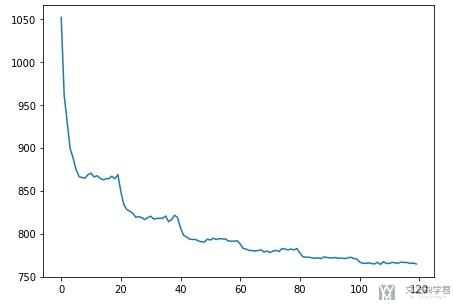
PyTorch使用记录02

不同的调节方法结合与CosineAnnealingLR介绍

上面我们介绍了关于Pytorch中动态调节学习率的方法, 这里会简单说明一下同时使用两种动态调节的方式，也会介绍一下另一种动态调节的方式，CosineAnnealingLR，会以周期性对lr进行变化。

我们需要注意的是，要想第二个动态学习率可以从第一个学习率之后进行调整, 我们需要在第一次调节完毕之后修改optimizer的initial learning rate，调节的方式如下:

  1. test_optimizer.param_groups[0]['initial_lr'] = test_optimizer.param_groups[0]['lr'] # 需要修改optimizer的initial lr

完整的实验代码如下

  1. from torch.optim import lr_scheduler
  3. test_optimizer = torch.optim.SGD([torch.randn(1, requires_grad=True)], lr=1e-3)
  5. exp_lr_scheduler = torch.optim.lr_scheduler.StepLR(test_optimizer, step_size=3, gamma=0.5)
  7. for epoch in range(1, 12):
  8.     exp_lr_scheduler.step() # 要每一个epoch都要使用
  9.     print('Epoch {}, lr {}'.format(
  10.         epoch, test_optimizer.param_groups[0]['lr']))
  12. print('='*10)
  13. test_optimizer.param_groups[0]['initial_lr'] = test_optimizer.param_groups[0]['lr'] # 需要修改optimizer的initial lr
  15. cos_lr_scheduler = torch.optim.lr_scheduler.CosineAnnealingLR(test_optimizer, T_max = 3, eta_min=0.00001)
  16. for epoch in range(12, 24):
  17.     cos_lr_scheduler.step() # 要每一个epoch都要使用
  18.     print('Epoch {}, lr {}'.format(
  19.         epoch, test_optimizer.param_groups[0]['lr']))

我们看一下learning rate的变化:

PyTorch使用记录02

调节算法MultiStepLR介绍

这是另外一种比较常用的自动调节学习率的方式, 是每次到了我们设置的milestones之后按照gamma来进行学习率的调整, 可以看下面简单的例子.

  1. >>> scheduler = MultiStepLR(optimizer, milestones=[30,80], gamma=0.1)
  2. >>> # Assuming optimizer uses lr = 0.05 for all groups
  3. >>> # lr = 0.05     if epoch < 30
  4. >>> # lr = 0.005    if 30 <= epoch < 80
  5. >>> # lr = 0.0005   if epoch >= 80

 

Pytorch中图片数据集处理方式

Pytorch中有比较简单的图片数据集的处理方式, 我们可以使用ImageFolder来完成图片数据集的导入. 下面我们来看一个简单的例子.

官方文档: ImageFolder介绍

  1. trans = transforms.Compose([
  2.     transforms.Resize(64),
  3.     transforms.ToTensor(),
  4.     transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))
  5. ])
  7. # 注意这里文件夹的路径
  8. dataset = datasets.ImageFolder('./data', transform=trans) # 数据路径
  9. dataloader = torch.utils.data.DataLoader(dataset,
  10.                                      batch_size=16, # 批量大小
  11.                                      shuffle=True, # 乱序
  12.                                      num_workers=2 # 多进程
  13.                                      )

同时我们需要注意的是, 这个类的root路径的书写. 他的文件格式是如下所示的.

  1. root/dog/xxx.png
  2. root/dog/xxy.png
  3. root/dog/xxz.png
  5. root/cat/123.png
  6. root/cat/nsdf3.png
  7. root/cat/asd932_.png

也就是他只需要写到root目录, 然后把每一类图片分别放在对应的文件夹内. 我们不能直接将图片放在root目录下, 不然就会出现如下的报错: RuntimeError: Found 0 images in subfolders of: ./data

上面报错解决链接: RuntimeError: Found 0 images in subfolders of: ./data

 

Pytorch中下划线的含义

关于Pytorch种下划线使用的情况, 详细的内容见下面的参考链接. 总的来说, 就是如果没有很大的内存压力, 就:

  • First of all on the PyTorch sites it is recommended to not use in-place operations in most cases. Unless working under heavy memory pressure it is more efficient in most cases to not use in-place operations.
  • Secondly there can be problems calculating the gradients when using in-place operations

下面看一个简单的例子, 就可以知道下划线加和不加的区别.

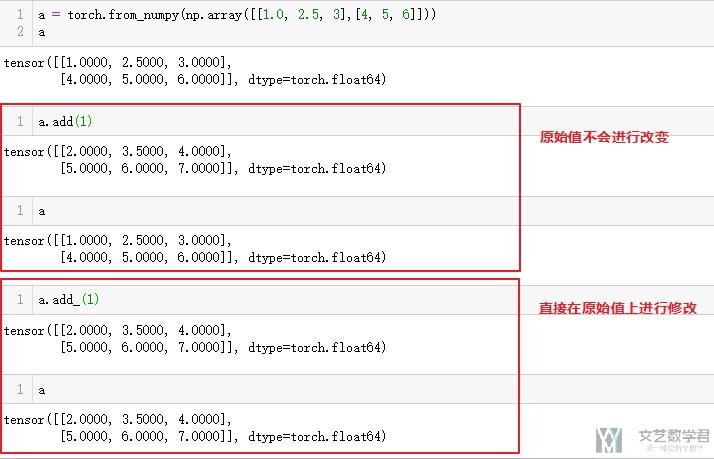
PyTorch使用记录02

参考资料: What does the underscore suffix in PyTorch functions mean?

 

Pytorch Tensor get the index of specific value(tensor获得指定值的index)

参考链接: How Pytorch Tensor get the index of specific value

我们有的时候会需要找出Tensor中特定值的index, 我们可以使用下面的方式进行寻找. 如下面的例子中, 我们想要找出value=1的位置所在.

  1. test = torch.Tensor([1,2,3,1,2,3,1,2,3])

我们可以使用nonzero()来完成相关操作.

  1. (test==1).nonzero().squeeze()
  2. """
  3. tensor([0, 3, 6])
  4. """

我们看一下完整的步骤, 下面有每一步操作的结果的显示.

PyTorch使用记录02

 

Pytorch中tensor的拼接

torch.cat测试

torch.cat可以用来合并两个tensor向量。我们下面简单举一个例子，这个是合并一维的向量.

  1. a = torch.tensor([])
  2. b = torch.tensor([1,2])
  3. c = torch.tensor([3,4,5])
  5. a = torch.cat((a,b))
  6. a = torch.cat((a,c))
  8. print(a)
  9. # >>> tensor([1., 2., 3., 4., 5.])

下面看一个稍微复杂的例子, 并看一下最终的效果。

  1. # torch.cat测试
  2. x_test = torch.tensor([[[0,1,0]],[[1,0,1]]])
  3. y_test = torch.tensor([[[2,2,2]],[[3,3,3]]])
  4. print(x_test.shape)
  5. print('===')
  7. print(torch.cat((x_test, y_test), dim=1))
  8. print(torch.cat((x_test, y_test), dim=1).shape)
  10. print('===')
  12. print(torch.cat((x_test, y_test), dim=0))
  13. print(torch.cat((x_test, y_test), dim=0).shape)

最终输出的结果如下所示，设置不同的dim合并的维度是不同的：

PyTorch使用记录02

我们可以看一下上面拼接前后shape的改变. 拼接前的shape分别是(2, 1, 3)和(2, 1, 3)， 拼接之后的shape为(4, 1, 3)如果dim=0的时候. 我们使用同样的数据使用torch.stack进行测试, 看一下两者有什么不同.

torch.stack测试

还是使用上面的x_test和y_test, 他们的shape都是(2, 1, 3), 我们看一下使用np.stack后的结果.

  1. torch.stack((x_test, y_test)).shape

使用之后的shape转换为torch.Size([2, 2, 1, 3]), 就是直接在外面堆叠. 这个在我们处理训练样本的时候, 可以使用这种方式将不同的样本合成一个batch. 如下面这个简单的例子.

  1. torch.stack(([dataset[i][0] for i in range(36)])).shape

torch.norm的简单使用说明

torch.norm是用来计算范数的, 我们简单来讲解一下用法.

关于范数的相关介绍, 可以查看以下的链接: 正则化技术介绍–L1,L2范数

其中的参数, p表示计算什么范数(l1范数, l2范数, 等), dim表示在哪一个维度进行计算. 下面看一个例子.

计算L1和L2范数, 我们还在最后验证了以下l2范数的计算的结果.

PyTorch使用记录02

除了上面使用torch.norm以外, 我们还可以按下面的方式进行使用.

PyTorch使用记录02

官方文档链接: Pytorch--torch.norm

中文的指南: torch.norm的理解

 

transform.Normalize()的简单介绍

参考资料: Understanding transform.Normalize( )

我们在进行图片的数据的时候, 有时会使用Normalize, 下面简单解释一下这个操作. 如下面的transforms.Normalize，我们对其进行解释.

  1. transform = transforms.Compose([
  2.                 transforms.ToTensor(),
  3.                 transforms.Normalize(mean=[0.5], std=[0.5])])

Normalize是进行下面的操作:  image = (image - mean) / std

在上面的例子中, mean=0.5, std=0.5, 这样使得image的范围变为[-1,1].

这是因为, 原始图片中最小值为0，于是(0-0.5)/0.5=-1变为了-1；最大值为1，(1-0.5)/0.5=1变换后还是1.

如果我们想要进行还原，可以使用下面的计算方式: image = ((image * std) + mean)

当mean=0.5, std=0.5的时候，我们可以写成下面的函数进行还原。

  1. def denorm(x):
  2.     out = (x + 1) / 2
  3.     return out.clamp(0, 1)

关于这么做是否可以使得结果变得更好, 现在不是很确定, 但是大部分的论文都是这么做的.

 

torch.gather使用

关于torch.gather的简单使用介绍. 关于gather的解释, 有一个很好的链接可以参考, 这里的图十分好懂, What does the gather function do in pytorch in layman terms? 里面赞最高的回答. 我在下面简答描述一下.

gather的主要用法如下图所示(这里和实际有一点不一样的地方, 这里下标是从1开始的, 实际上下标应该是从0开始的, 后面看代码的时候会有看到).

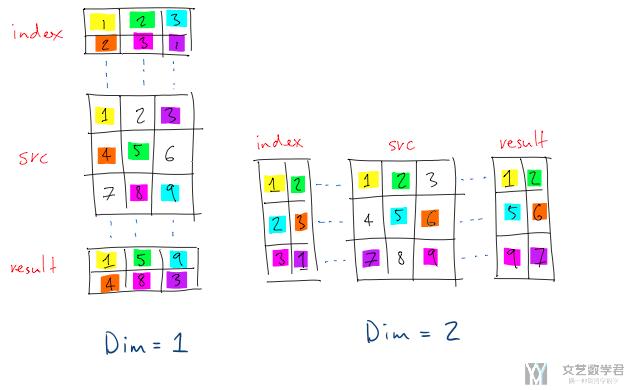
PyTorch使用记录02

首先我们看左侧, 也就是dim=1的部分. dim=1时我们看一列(竖着看). index的第一列是1和2, 我们于是在src中的第一列找出第一和第二个元素, 放入result. index的第二列是2,3, 我们于是在src的第二列中找出第二和第三个元素, 放入result中, 第三列以此类推.

接着我们看右侧, 也就是dim=2的部分. dim=2时我们看一行(横着看). index的第一行是1和2, 于是我们在src的第一行找出第1和第2个元素放入result. index的第二行是2,3, 我们于是在src的第二行中找出第二和第三个元素5和6, 放入result中, 第三行以此类推.

下面我们看一下实际的代码, 注意这里的代码是从0开始的, 但是意思的理解是和上面是一样的. dim=0代表是列, 也就是上面的dim=1的对应方式, 可以自行比较一下.

  1. src = torch.tensor([[1,2,3],[4,5,6],[7,8,9]]).float()
  2. indexV = torch.tensor([[1,2,0],[2,0,1],[1,2,0]]).long()
  3. # dim=0测试
  4. torch.gather(input=src, dim=0, index=indexV)
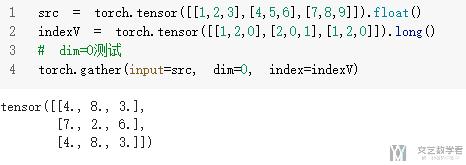
PyTorch使用记录02

 

dim=1代表是行, 也就是上面的dim=2的对应方式, 可以自行比较一下.

  1. src = torch.tensor([[1,2,3],[4,5,6],[7,8,9]]).float()
  2. indexV = torch.tensor([[1,2,0],[2,0,1],[1,2,0]]).long()
  3. # dim=1测试
  4. torch.gather(input=src, dim=1, index=indexV)
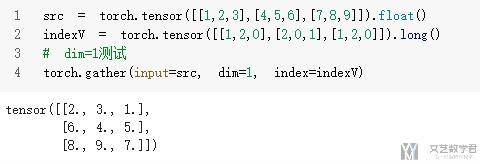
PyTorch使用记录02

 

torch中常见的计算

torch.dot-Pytroch中向量与向量乘法

两个向量相乘就是逐个元素相乘进行求和.

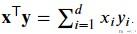
PyTorch使用记录02

下面我们来看一个简单的例子.

  1. x = torch.arange(4, dtype=torch.float32)
  2. y = torch.ones(4, dtype = torch.float32)
  3. x, y, torch.dot(x, y)
  4. """
  5. (tensor([0., 1., 2., 3.]), tensor([1., 1., 1., 1.]), tensor(6.))
  6. """

 

torch.mv-Pytorch中矩阵与向量乘法

这里mv就是表示Matrix-Vector Products. 如果A是一个矩阵, 每一行我们都用向量表示. x是一个向量, A和x进行乘法运算.

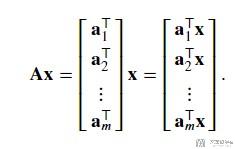
PyTorch使用记录02

我们看下面一个例子.

  1. x = torch.arange(4, dtype=torch.float32)
  2. A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
  3. torch.mv(A, x)
  4. """
  5. tensor([ 14.,  38.,  62.,  86., 110.])
  6. """

 

torch.mm-Pytorch中的矩阵乘法

我们可以使用torch.mm来完成矩阵乘法. 这里的mm就是表示matrix * matrix下面看一个简单的例子.

  1. a = torch.from_numpy(np.array([[0,1,0],[1,0,1]]))
  2. b = torch.from_numpy(np.array([[1,4],[2,5],[3,6]]))

最后的计算结果如下, 上面是一个2 3的矩阵乘3 2的矩阵, 结果是一个2 * 2的矩阵.

  1. torch.mm(a,b)
  2. """
  3. tensor([[ 2,  5],
  4.         [ 4, 10]], dtype=torch.int32)
  5. """

 

torch.mul--Pytorch中对应位相乘

我们可以使用torch.mul来完成矩阵的对应位置的相乘. 他的操作如下图所示:

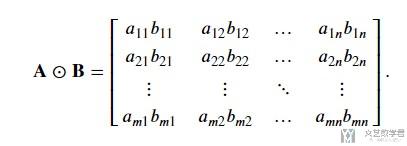
PyTorch使用记录02

我们可以看下面的一个例子.

  1. a = torch.from_numpy(np.array([[0,1,0],[1,0,1]]))
  2. b = torch.from_numpy(np.array([[1,2,3],[4,5,6]]))

我们进行计算, 得到如下的结果.

  1. torch.mul(a,b)
  2. """
  3. tensor([[0, 2, 0],[4, 0, 6]], dtype=torch.int32)
  4. """

可以看到结果是对应位进行了相乘, 1的地方还是保留了原来的数值. 这个操作是和ab是相同的, 在Pytorch中, 使用ab就是对应位置元素相乘.

同样, 我们可以将mul直接写在数字后面, 进行相乘. 看下面的一个例子. 我们先将所有的数字乘0.5, 再求指数.

  1. torch.from_numpy(np.array([-1.0,2.0,10.0])).mul(0.5).exp()
  2. """
  3. tensor([  0.6065, 2.7183, 148.4132], dtype=torch.float64)
  4. """

 

torch.bmm-Pytorch中的batch的矩阵乘法

下面我们看一下在Pytorch中如何进行batch矩阵乘法。我们测试的矩阵乘法如下所示, 我们简单说明一下, 下面是213, 231, 得到的结果是211. (这个也就是在batch内部, 还是在进行矩阵乘法)

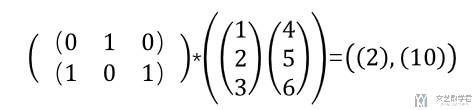
PyTorch使用记录02

我们使用Pytorch做以下测试，可以看到结果是和我们自己计算是一样的。

  1. # torch.bmm测试-这是矩阵乘法
  2. x_test = torch.tensor([[[0,1,0]],[[1,0,1]]])
  3. y_test = torch.tensor([[[1],[2],[3]],[[4],[5],[6]]])
  5. print(x_test.shape,y_test.shape)
  6. print(torch.bmm(x_test,y_test))
  7. """
  8. torch.Size([2, 1, 3]) torch.Size([2, 3, 1])
  9. tensor([[[ 2]],
  11.         [[10]]])
  12. """

参考资料: torch.bmm官方文档

 

Pytorch生成随机数

生成服从正态分布的随机数

我们生成指定形状的正态分布的数据. 我们可以直接传入tensor的size.

  1. a = torch.from_numpy(np.array([[1,2,3],[4,5,6]]))
  2. torch.randn(*a.size())
  3. """
  4. tensor([[-2.4163, -0.9349, -0.1467],
  5.         [-1.4294, -0.3001,  0.7097]])
  6. """

 

生成整数随机数

除了上面的方式之后, 我们还可以直接再后面跟random来生成随机数. 同样, 我们首先使用torch.ones来生成指定的形状, 接着在生成随机数.

  1. torch.ones([3, 3], dtype=torch.float64).random_(10, 20)
PyTorch使用记录02

参考资料: Random integers

 

Softmax的一些用法

Softmax的dim的一些说明

这里说一下nn.Softmax中的dim的一些说明。

  1. # Softmax测试
  2. x_test = torch.tensor([[[0,1,0]],[[1,1,1]]]).float()
  3. print(x_test.shape)
  4. F.softmax(x_test,dim=2)
  5. """
  6. torch.Size([2, 1, 3])
  7. tensor([[[0.2119, 0.5761, 0.2119]],
  9.         [[0.3333, 0.3333, 0.3333]]])
  10. """

这里设为了dim=2，即对最里面的内容进行softmax求解。

Softmax与LogSoftmax

关于这两者的比较，可以查看这一篇文章，Softmax v.s. LogSoftmax。

简单说一下就是当如果在softmax_xi很大的情況下（接近1)，比如說0.999，那整個反向傳遞就會多乘上(0.999)(1–0.999)=0.999*0.001=0.000999，這代表你的誤差整整縮小超過1000倍，除非loss本身就很大，不然整體網路的訓練效果會非常非常差．

同理在softmax_xi很小（接近0）的情況下也會有一樣的情況．(详细看上面的文章)

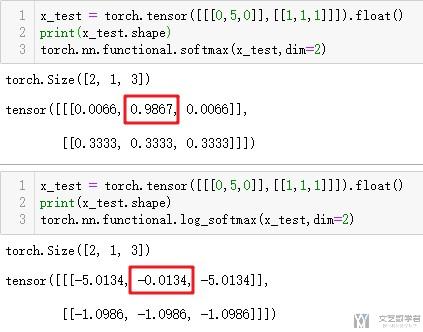
但是使用LogSoftmax越接近0相当于之前Softmax越接近于1的情况。我们可以看到下面的演示，使用softmax的时候, 越接近1，在使用log_softmax的时候就越接近于0.

PyTorch使用记录02

weight clip的用法

有的时候我们在训练网络的时候, 我们会进行梯度裁剪, 下面简单看以下梯度裁剪的例子.

  1. a = torch.tensor([-1.1, 0.8, 1.2, -0.6, 0.9])
  2. a.data.clamp_(-1, 1) # 这个是可以改变原始的a的

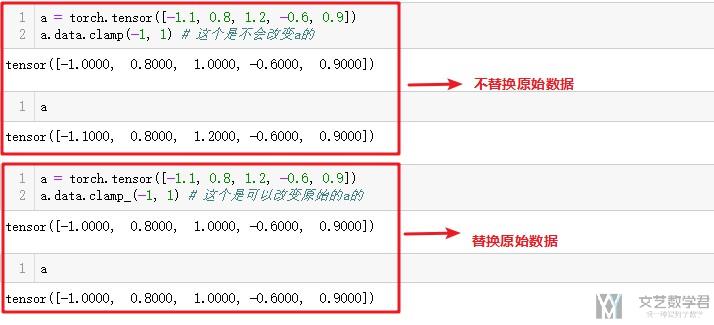
上面的意思是将a的data裁剪在范围是(-1, 1)之间. 下面看一下完整的图片.

PyTorch使用记录02

torch.autograd简单使用

官方链接: AUTOMATIC DIFFERENTIATION PACKAGE - TORCH.AUTOGRAD

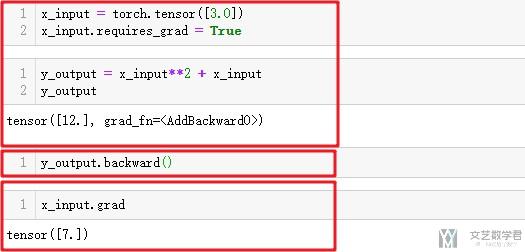
这里会介绍两个函数, 分别是torch.autograd.backward和torch.autograd.grad. 看一下两个使用的例子. 我们定义一个函数为, f(x)=x^2+x.

torch.autograd.grad

这个会在WGAN-GP中使用, 计算penalty gradient的时候, 我们可以理解为他是计算某个特定的x的梯度的.

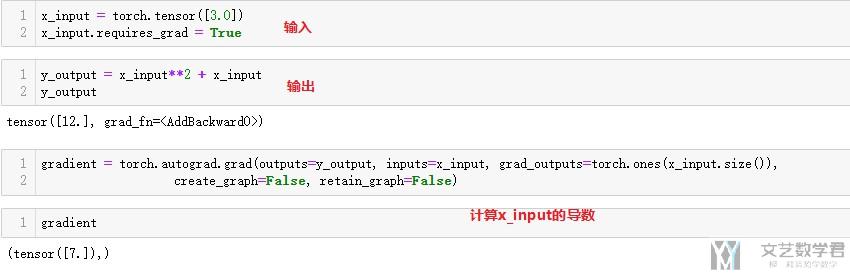
PyTorch使用记录02

torch.autograd.backward

我们可以理解为他是计算整个计算图上每一个变量的梯度. 还是上面相同的例子, 计算出的x_input处的梯度也是相同的.

PyTorch使用记录02

Using pad_packed_sequence in Pytorch

在RNN的训练中，我们有的时候需要进行padding, 从而才可以使用batch进行训练。但是这样，我们需要在后面填充0.会对最后的结果有所影响，所在在Pytorch中可以使用pack_padded_sequence()和pad_packed_sequence()来处理变长的序列。压缩的过程如下所示。

具体的说明可以看一下链接 : Pytorch中如何处理RNN输入变长序列padding

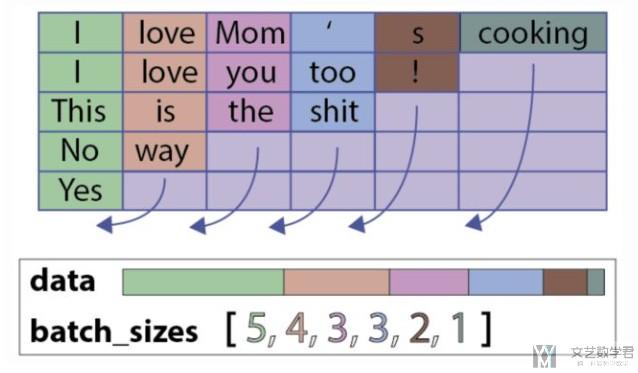
PyTorch使用记录02

需要说明一下，这么做首先也是需要进行padding的(看上图), 只不过会需要记住在padding之前，每句话的原始长度。

下面看一下在如何将pack_padded_sequence()和pad_packed_sequence()加在整个训练的过程中去。

  1. pack_padded_sequence(batch_in, seq_lengths, batch_first=True)

在使用pack_padded_sequence的时候, 需要注意batch_in中的length需要按从大到小的顺序进行排序, 第二个参数seq_length表示batch中每一句话的长度。

下面是一个整体的流程：How to use pad_packed_sequence in pytorch

  1. # SORT YOUR TENSORS BY LENGTH!(按长度进行排序)
  2. seq_lengths, perm_idx = seq_lengths.sort(0, descending=True)
  3. seq_tensor = seq_tensor[perm_idx]
  5. # utils.rnn lets you give (B,L,D) tensors where B is the batch size, L is the maxlength, if you use batch_first=True
  6. # Otherwise, give (L,B,D) tensors
  7. seq_tensor = seq_tensor.transpose(0,1) # (B,L,D) -> (L,B,D)
  9. # embed your sequences(embedding)
  10. seq_tensor = embed(seq_tensor)
  12. # pack them up nicely
  13. packed_input = pack_padded_sequence(seq_tensor, seq_lengths.cpu().numpy())
  15. # throw them through your LSTM (remember to give batch_first=True here if you packed with it)
  16. packed_output, (ht, ct) = lstm(packed_input)
  18. # unpack your output if required
  19. output, _ = pad_packed_sequence(packed_output)
  20. print (output)
  22. # Or if you just want the final hidden state?
  23. print (ht[-1])

下面是一段我在实际使用的时候写的，我们主要看forward的部分。

  1. class ClickSingleGRU(nn.Module):
  2.     def __init__(self, vocab_size, embedding_dim, hidden_units, batch_sz, output_size, layers=2, Drop_switch=False):
  3.         super(ClickSingleGRU, self).__init__()
  4.         self.Drop_switch = Drop_switch # 是否使用dropout
  5.         self.vocab_size = vocab_size # 总的单词的个数
  6.         self.embedding_dim = embedding_dim # embedding之后的元素个数
  7.         self.hidden_units = hidden_units # GRU中的hidden units的个数
  8.         self.batch_sz = batch_sz
  9.         self.output_size = output_size
  10.         self.num_layers = layers # GRU的layers
  11.         # layers
  12.         self.embedding = nn.Embedding(self.vocab_size, self.embedding_dim) # 可以将标号转为向量
  13.         self.dropout = nn.Dropout(0.5)
  14.         self.gru = nn.GRU(self.embedding_dim, self.hidden_units, num_layers=self.num_layers, batch_first = True, bidirectional=True, dropout=0.5)
  15.         self.fc = nn.Linear(self.hidden_units*2, self.output_size)
  16.         self.batchNorm = nn.BatchNorm1d(self.hidden_units*2)
  18.     def init_hidden(self):
  19.         # 使用了双向RNN, 所以num_layer*2
  20.         return torch.zeros((self.num_layers*2, self.batch_sz, self.hidden_units)).to(device1)
  22.     def forward(self, x, x_len):
  23.         x = x.to(device1)
  24.         # 按照顺序进行排序
  25.         _, perm_idx = x_len.sort(0, descending=True)
  26.         x = x[perm_idx] # 对样本x重新排序
  27.         x_len = x_len[perm_idx] # 对长度x重新排序
  29.         # 进行正向传播
  30.         self.batch_sz = x.size(0)
  31.         x = self.embedding(x)
  32.         # print(x.shape)
  33.         # print(x_len)
  34.         x = pack_padded_sequence(x, x_len, batch_first=True)
  35.         self.hidden = self.init_hidden()
  36.         output, self.hidden = self.gru(x, self.hidden)
  37.         output, _ = pad_packed_sequence(output, batch_first=True)
  38.         # print(output.shape)
  39.         # 因为是 batch*seq*output, 所以要取最后一个seq
  40.         output = output[:,-1,:]
  41.         # print(output.shape)
  42.         if self.Drop_switch:
  43.             output = self.dropout(output)
  44.         output = self.batchNorm(output)
  45.         output = self.fc(output)
  46.         # print(output.shape)
  48.         # 对输出重新排序, 这个需要与最后的label对应上
  49.         output = output[perm_idx]
  50.         # print(output.shape)
  51.         return output

forward会传入两个参数，一个是要训练的文本(这个是padding之后的，一个batch)，x_len表示这个batch中每句话的实际长度。

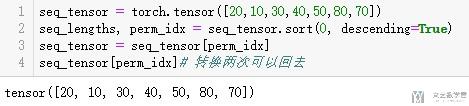
之后首先就先按x_len的大小, 对x和x_len进行排序。进行传播后，最后还需要还原为原来的x的顺序，需要和label的顺序对应上。

下面图片可以看到，进行两次转换之后可以还原。

PyTorch使用记录02

  • 微信公众号
  • 关注微信公众号
  • weinxin
  • QQ群
  • 我们的QQ群号
  • weinxin
王 茂南
  • 本文由 发表于 2019年6月14日07:59:21
  • 转载请务必保留本文链接：https://mathpretty.com/10594.html
匿名

发表评论

匿名网友 填写信息

:?: :razz: :sad: :evil: :!: :smile: :oops: :grin: :eek: :shock: :???: :cool: :lol: :mad: :twisted: :roll: :wink: :idea: :arrow: :neutral: :cry: :mrgreen: